- 递减数列

递减数列
基本介绍
一个实数列{an},如果从第二项起,每一项都不大于它的前一项,即有
![]()
这样的实数列叫递减数列也叫下降数列或说这一数列单调下降,例如,数列0.1,0.01,0.001,0.0001.…和数列2,1,0,-1,-2,…等都为递减数列。
如果每一项都小于它的前一项,即a
![]()
则这样的实数列叫严格递减数列,或说这一数列严格单调下降,例如-2,-4,-6,…,-2n,…即是严格递减数列[1]。
相关介绍
若数列![]() 从第二项起,每一项都大或等于它前面的一项,即对于任何自然数n,都有
从第二项起,每一项都大或等于它前面的一项,即对于任何自然数n,都有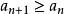 ,则数列
,则数列![]() 叫做不减的,或叫做(广义)递增数列,例如数列
叫做不减的,或叫做(广义)递增数列,例如数列
2,4,4,8,8,8,16,16,16,16,...; (1)
![]() 的精确到0.1,0.01,0.001,0.0001, ... 的不足近似值组成的数列
的精确到0.1,0.01,0.001,0.0001, ... 的不足近似值组成的数列
1.4,1.41,1.414,1.4142,...; (2)
1,2,3,4,5,...; (3)
![]() 2,4,8,...,2n,... (5)
2,4,8,...,2n,... (5)
都是(广义)递增数列[2]。
若数列![]() 从第二项起,每一项都大于它前面的一项,即对任何自然数n, 都有
从第二项起,每一项都大于它前面的一项,即对任何自然数n, 都有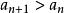 ,则数列
,则数列![]() 叫做严格递增数列。例如上面的数列(2),(3),(4),(5)都是严格递增数列。
叫做严格递增数列。例如上面的数列(2),(3),(4),(5)都是严格递增数列。
 递推公式若数列
递推公式若数列![]() 从第二项起,每一项都小于或等于它前面的一项,即对任何自然数n,都有
从第二项起,每一项都小于或等于它前面的一项,即对任何自然数n,都有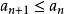 ,则数列
,则数列![]() 叫做不增的,或叫做(广义)递减数列,例如数列
叫做不增的,或叫做(广义)递减数列,例如数列
![]()
![]() 的精确到0.1,0.01,0,001, 0.0001, ..的过剩近似值组成的数列
的精确到0.1,0.01,0,001, 0.0001, ..的过剩近似值组成的数列
1.5,1.42, 1.415,1.4143,...; (7)
![]()
![]() 都是(广义)递减数列。
都是(广义)递减数列。
若数列![]() 从第二项起,每一项都小于它前面的一项,即对任何自然数n,都有
从第二项起,每一项都小于它前面的一项,即对任何自然数n,都有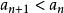 ,则数列
,则数列![]() 叫做严格递减数列。例如上面的数列(7),(8),(9)都是严格递减数列。
叫做严格递减数列。例如上面的数列(7),(8),(9)都是严格递减数列。
(广义)递增数列和(广义)递减数列统称为(广义)单调数列。
严格递增数列和严格递减数列统称为严格单调数列[2]。

-
追逐爱情,三十减去三
2025-10-04 01:31:08 查看详情 -
首推两款车型/轴距或与沃尔沃XC90接近 节能减排出新招
2025-10-04 01:31:08 查看详情 -
长城炮为你硬核助攻 实力不减
2025-10-04 01:31:08 查看详情 -
江铃新宝典VS长城风骏7(图文) 实力不减
2025-10-04 01:31:08 查看详情 -
成都长城哈弗H6现车充足 实力不减
2025-10-04 01:31:08 查看详情 -
长城炮乘用皮卡全球版 实力不减
2025-10-04 01:31:08 查看详情 -
长城欧拉iQ怎么样 实力不减
2025-10-04 01:31:08 查看详情 -
皮卡顶流长城炮 实力不减
2025-10-04 01:31:08 查看详情


 求购
求购




