- 笛卡尔乘积

笛卡尔乘积
笛卡儿积的性质
易见笛卡儿积满足下列性质:
对于任意集合![]() ,根据定义有
,根据定义有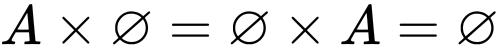
一般来说笛卡儿积不满足交换律和结合律。
笛卡儿积对集合的并和交满足分配律,即
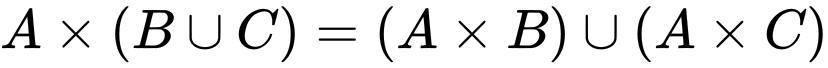
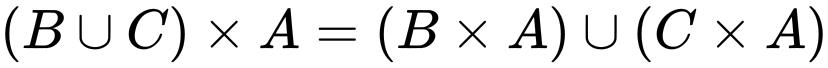
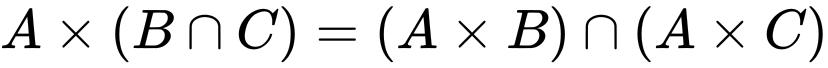
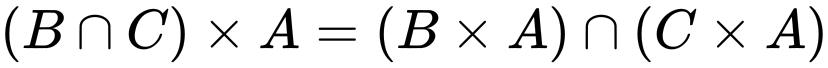
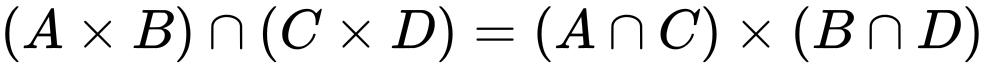
笛卡儿平方和n元乘积
集合![]() 的笛卡儿平方(或二元笛卡儿积)是笛卡儿积
的笛卡儿平方(或二元笛卡儿积)是笛卡儿积 。一个例子是二维平面,(这里
。一个例子是二维平面,(这里![]() 是实数集) - 它包含所有的点
是实数集) - 它包含所有的点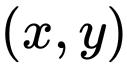 ,这里的
,这里的![]() 和
和![]() 是实数(参见笛卡儿坐标系)。
是实数(参见笛卡儿坐标系)。
为了帮助枚举,可绘制一个表格。一个集合作为行而另一个集合作为列,从行和列的集合选择元素,以形成有序对作为表的单元格。
可以推广到在![]() 个集合上的n-元笛卡儿积:
个集合上的n-元笛卡儿积:
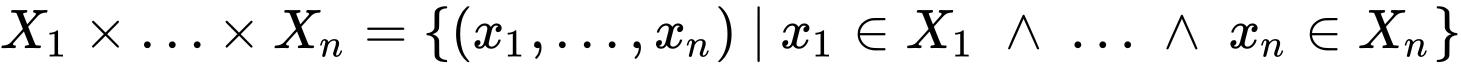 。
。
实际上,它可以被等同为。它是n-元组的集合。
一个例子是欧几里得三维空间,这里的![]() 同样是指实数集。
同样是指实数集。
无穷乘积
对最常用的数学应用而言,上述定义通常已经足够。但是,也可以在任意(可能无限)的集合的搜集上定义笛卡儿积。如果![]() 是任何指标集合,而
是任何指标集合,而
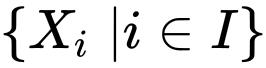
是由![]() 索引的集合的搜集,则我们定义
索引的集合的搜集,则我们定义
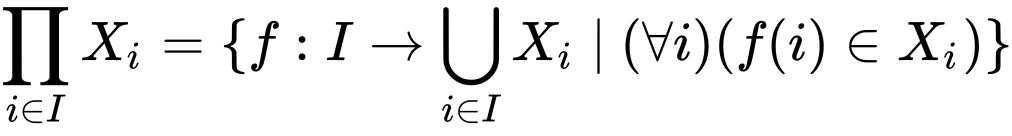 ,
,
就是定义在索引集合上的所有函数的集合,使得这些函数在特定索引![]() 上的值是
上的值是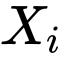 的元素。
的元素。
对在![]() 中每个
中每个![]() ,定义自
,定义自
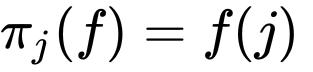
的函数
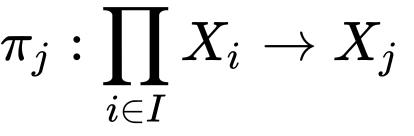
叫做第![]() 投影映射。
投影映射。
n-元组可以被看作在上的函数,它在![]() 上的值是这个元组的第
上的值是这个元组的第![]() 个元素。所以,在
个元素。所以,在![]() 是的时候,这个定义跟有限情况的定义是一致的。在无限情况下这个定义给出的是集合族。
是的时候,这个定义跟有限情况的定义是一致的。在无限情况下这个定义给出的是集合族。
在无限情况,一个令人熟悉的特例是,当索引集合是自然数集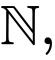 的时候:这正是其中第i项对应于集合
的时候:这正是其中第i项对应于集合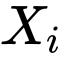 的所有无限序列的集合。再次,
的所有无限序列的集合。再次,![]() 提供了这样的一个例子:
提供了这样的一个例子:
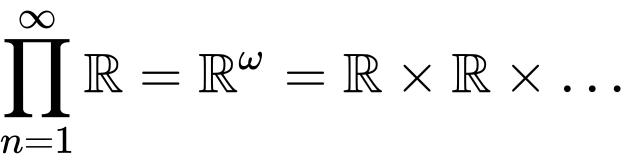
是实数的无限序列的搜集,可视之为带有无限个构件的向量或元组。另一个特殊情况(上述例子也满足它)是在乘积中的各因子Xi都是相同的时候,类似于“笛卡儿指数”。这样,在最先定义中的无限并集自身就是这个集合自身,而其他条件被平凡的满足了,所以这正是从I到X的所有函数的集合。
在别的情况,无限笛卡儿积就不那么直观了;尽管在高等数学中的应用有其价值。
“非空集合的任意非空搜集的笛卡儿积为非空”这一陈述等价于选择公理。
函数的笛卡儿积
如果![]() 是从
是从![]() 到
到![]() 的函数,而
的函数,而![]() 是从
是从![]() 到
到![]() 的函数,则它们的笛卡儿积是从到的函数,带有
的函数,则它们的笛卡儿积是从到的函数,带有
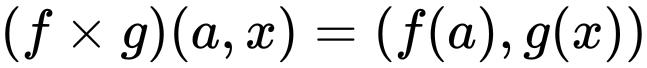
跟之前类似,函数的笛卡儿积也可以扩展到函数的元组和无限情况。

-
卡尔·弗里德里希·本茨
2025-10-23 12:00:52 查看详情


 求购
求购










