n阶行列式

n阶行列式(4)按照一定的规则，由排成正方形的一组(n个)数(称为元素)之乘积形成的代数和，称为n阶行列式。

例如，四个数a、b、c、d所排成二阶行式记为，它的展开式为ad-bc。

九个数a1，a2，a3;b1，b2，b3;c1，c2，c3排成的三阶行列式记为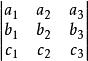，它的展开式为a1b2c3+a2b3c1+a3b1c2-a1b3c2-a2b1c3-a3b2c1. 行列式起源于线性方程组的求解，在数学各分支有广泛的应用。在代数上，行列式可用来简化某些表达式，例如表示含较少未知数的线性方程组的解等。

在1683年，日本的关孝和最早提出了行列式的概念及它的展开法。莱布尼兹在1693年(生前未发表)的一封信中，也宣布了他关于行列式的发现。^[3]

定义1 n阶行列式

等于所有取自不同行不同列的n个元素的乘积

的代数和，这里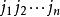是1,2，...，n的一个排列，每一项都按下列规则带有符号：当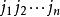是偶排列时带有正号，当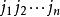是奇排列时带有负号。这一定义可写成

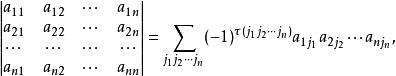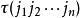这里表示对所有n级排列求和，表示排列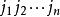的逆序数。

由定义1立即看出，n阶行列式是由n! 项组成的。^[1]

性质1 行列互换，行列式不变。

性质2 把行列式中某一行（列）的所有元素都乘以一个数K，等于用数K乘以行列式。

性质3 如果行列式的某行(列）的各元素是两个元素之和，那么这个行列式等于两个行列式的和。

性质4 如果行列式中有两行（列）相同，那么行列式为零。（所谓两行（列）相同就是说两行（列）的对应元素都相等）

性质5 如果行列式中两行（列）成比例，那么行列式为零。

性质6 把一行（列）的倍数加到另一行（列），行列式不变。

性质7 对换行列式中两行（列）的位置，行列式反号。^[1]

首先给出代数余子式的定义。

定义2^[1]在行列式

中划去元素aij所在的第i行第j列，剩下的(n-1)2个元素按原来的排法构成一个n-1阶的行列式Mij，称Mij为元素aij的余子式，Aij=(-1)i+jMij称为元素的代数余子式。

定理^[1]设

Aij表示元素aij的代数余子式，则下列公式成立：

行列式

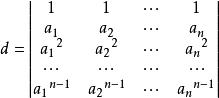称为n级的范德蒙德（Vandermonde）行列式。可以证明：对任意的 n（n≥2），n阶范德蒙德行列式等于a1，a2，...，an这n个数的所有可能的差ai-aj（1≤j<i≤n）的乘积。^[1]