单形

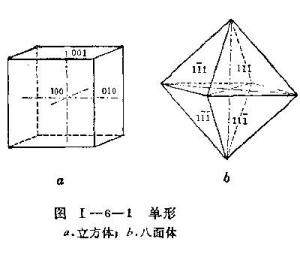同一单形的所有 晶面彼此都是等同的。所谓等同，是指它们具有相同的性质以及在 理想的情况下晶面彼此同形等大。如图中所示的单形为 立方体，它的六个 正方形晶面同形等大，通过其 对称型中的 对称要素的作用可以相互重复。

总结起来，在 几何形态上不同的 单形共有47种，称为 几何单形。

47种 几何单形如下：

低 级晶族：单面， 平行双面，反映双面及轴双面，斜方柱，斜方 四面体，斜方 单锥，斜方双锥。

中级晶族:三方柱，复三方柱，四方柱，复四方柱，六方柱，复六方柱；

三方 单锥，复三方单锥，四方单锥，复四方单锥，六方单锥，复六方单锥；

三方双锥，复三方双锥，四方双锥，复四方双锥，，六方双锥，复六方双锥；四方 四面体，菱面体，复四方偏三角面体，复三方偏三角面体；

三方偏方面体（具左、右形），四方偏方面体（具左、右形），六方偏方面体（具左、右形）。

高级晶族： 四面体， 三角三四面体，四角三四面体，五角三四面体（具左、右形），六四面体；

八面体， 三角三八面体， 四角三八面体，五角三八面体（具左、右形），六八面体；

立方体， 四六面体， 菱形十二面体， 五角十二面体，偏方复十二面体。

单形

如果不仅考虑 几何形态，同时还要考虑其 对称性的话，则单形共有146种，称为 结晶单形。

单形符号简称形号，它是指在单形中选择一个代表面，把该晶面的 晶面指数用{}括起来，用以表征组成该单形的一组晶面的 结晶学取向的符号。

单形是由 对称要素联系起来的一组 晶面， 晶轴是在服从 晶体固有对称性的前提下，依对称要素选择的。因此，同一单形的各个 晶面与 晶轴都有着基本相同的相对位置。如图I一6—1中的 立方体的每一个晶面都与一个 晶轴垂直而与另两个晶轴平行； 八面体的每一个晶面都截三个晶轴等长。因此，同一单形的各个晶面的指数的 绝对值不变，而只有 正负号的区别。如 立方体有六个晶面，其 晶面符号应分别为(100)、(010)、(001)、(-100)、(0-10)、(00-1)(在图I－6－1a中后三个晶面符号末标出)； 八面体有八个晶面，其晶符号应分别为(111)、(1-11)、(11-1)、(1-1-1)、(-111)、(-1-11)、(-11-1)、(-1-1-1)(图I－6－1b中后四个晶面符号未标出)。知道了单形的一个晶面的符号，则该单形的其它晶面的符号即可导出。因此，可以选择一个代表晶面，定出单形符号，如 立方体的形号为{100}， 八面体的形号为{111}等。

习惯上，选择代表晶面定形号时，一般是选择正指数最多的晶面，同时还遵循先前(即x轴上指数最大)、次右(即Y轴上的指数次大)、后上(即z轴上的指数最小)的原则。

各种单形的形号列于表I-6-1。依据形号，可以帮助我们识别聚形中的单形。

单形的各个 晶面既然可以通过 对称型中 对称要素的作用相互重复，那么将一个原始晶面置于对称型中，通过对称型中全部对称要素的作用，必可以导出一个单形的全部晶面。

可以设想，不同的 对称型可以导出不同单形；在同一对称型中原始晶面与 对称要素的相对位置不同，也可以导出不同的单形来。

几何单形共47种。从不同的角度出发，又可将它们做如下的几种划分。

一般形与特殊形，开形和闭形， 左形和右形，正形和负形，定形和变形 1)一般形与特殊形

?这是根据单形晶面与 对称要素的 相对位置来划分的。凡是单形晶面处于特殊位置，即晶面垂直或平行于任何 对称要素，或者与相同的对称要素以 等角相交，则这种单形即称为特殊形；反之，单形晶面处于一般位置，即不与任何对称要素垂直或平行(等轴晶系中的一般形有时可平行三次轴的情况除外)，也不与相同的对称要素以等角相交，则这种单形称为一般形。

一个 对称型中，只可能有一种一般形，晶类即以其一般形的名称来命名(参看晶体分类)。各 对称型中所列出的第一个单形即为该对称型的一般形。

(2)开形和闭形

根据单形的 晶面是否可以自相闭合来划分，凡是单形的晶面不能封闭一定空间者称开形，例如 平行双面、各种柱等等；反之，凡是其晶面可以封闭一定空间者，则称为闭形．例如各种双锥以及等轴晶系的全部单形等等。

(3) 左形和右形

互为 镜象，但不能以旋转操作使之重合的两个图形，称为左右形。 从 几何形态来看偏方面体、五角三 四面体和五角三 八面体都有 左形和右形之分。识别它们的左右可采用如下的办法。

对于偏方面体，可以上部晶面的两个不等长的边为准，长边在左者为 左形，长边在右者为右形。

对五角三 四面体(图I一6—7)，在其两个L3的出露点之间可以找到由三条 晶棱组成的一条 折线，我们还可以联系两个L3的出露点再作一条假想的 直线来辅助观察，若组成折线的最下边的一条晶梭偏向左上方，即为 左形；反之，即为右形。 对于五角三 八面体(图I一6—8)，在其两个L4的出露点之间也可找到由三条晶棱组成的一条折线，我们再联系该两个L4的出露点作一条假想 直线来辅助观察，若折线中最上边的一条晶棱偏向直线的左下方，即为左形；反之，则为右形。左右形只出现于仅具 对称轴而不具 对称面、 对称中心和 旋转反伸轴的 对称型中。若不仅考虑外形而同时考虑其本身的对称性的话，则属于这类 对称型的全部单形应均有 左形和右形的区分。

(4)正形和负形 取向不同的两个相同的单形，如果相互间能借助旋转操作而彼此重合者，则互为正负形。例如图I一6—9和图I一6—10分别表示出 四面体和五角十二面的正形和负形，它们的负形相当于正形旋转了90。。

(5)定形和变形

一种单形其 晶面间的角度为 恒定者，属于定形；反之，即为变形。属于定形者有单面、 平行双面、三方柱、四方往、六方柱、 四面体、 立方体、 八面体和 菱形十二面体九种单形；其余单形皆为变形。以变形 五角十二面体为例，图I一6—11表示了它的面角随 晶面指数的不同而变化。