最小公倍式

最小公倍式是整数环中最小公倍数概念的推广，如果多项式m(x)满足：

1.m(x)是多项式f(x)与g(x)的公倍式，即f(x)|m(x)，且g(x)|m(x)；

2.f(x)与g(x)的任一个公倍式都是m(x)的倍式；

则称m(x)为f(x)与g(x)的最小公倍式，两个不全为零的多项式f(x)与g(x)的最小公倍式中首项系数为1的最小公倍式常用[f(x)，g(x)]表示，P[x]中非零多项式f(x)，g(x)的最小公倍式与最大公因式的关系是

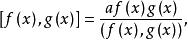式中a是f(x)与g(x)的首项系数乘积的倒数^[1]。

定理1设φ(x)与k(x)都是f(x)与g(x)的最小公倍式,则φ(x)与k(x)只能相差一个非零常数因子^[2]。

证明因为k(x)是公倍式,φ(x)是最小公倍式，故：

φ(x)|k(x)，

同理:

k(x)|φ(x)，

所以，k(x)与φ(x)只能相差一个非零常数因子。

定理2若φ(x)是f(x)与g(x)的最小公倍式，c≠0，则cφ(x)也是f(x)与g(x)的最小公倍式。

证明首先cφ(x)是f(x)与g(x)的公倍式，此外，若k(x)是f(x)与g(x)的任一公倍式，则由于：

φ(x)|k(x)，

必有：

cφ(x)|k(x)，

因而cφ(x)是最小公倍式。

推论1设φ(x)=[f(x),g(x)],则f(x)与g(x)的最小公倍式是且仅是cφ(x)(c≠0)形式的多项式。

定理3若f(x)|g(x),则[f(x)，g(x)] =g(x)。

定理4若(f(x),g(x)) =1，则[f(x)，g(x)]=f(x)g(x)。

定理5设f(x)和g(x)是数域P.上的非零多项式,d(x)和φ(x)分别是其最大公因式与最小公倍式，则d(x)φ(x)与f(x)g(x)相差一个非零常数因子，即存在c∈P，c≠0，使d(x)φ(x) =cf(x)g(x)。

推论2两个多项式f(x)与g(x)的最大公因式与最小公倍式的积等于这两个多项式的积，即(f(x),g(x)[f(x),g(x)]=f(x)·g(x)^[2]。

求最小公倍式的技能指利用两个 多项式的最大公因式求它们的最小公 倍式，或利用各多项式(大于零次)的标准分解式求其最小公倍式的技能。 它是分式运算中通分的基础^[3]。

求最小公倍式技能训练的基本要 求和注意点是：

①会利用两个非零多项式的最大公因式求它们的最小公倍 式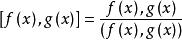：。但这 一方法不能推广到求多个非零多项式的最小公倍式，因为一般的

[f(x)，g(x)，h(x)](f(x)，g(x)，h(x)) ≠f(x)，g(x)，h(x)。

②会通过逐次求两个多项式的最小公倍式来求得两个以上多项式的最小公倍式。

③会利用所给大于零次的各多项式的标准分解式，求它们的最小公倍式。这时要取各多项式的所有不可约因式， 且幂指数要取它在各标准分解式中的最高次数，所有这样不可约因式方幂的积才是所求的最小公倍式。并懂得 这一方法的使用是有条件的，需要能求得各个多项式的标准分解式才行， 而这常常是办不到的。

④对于具体问题，能根据所给多项式或条件，选取恰当的方法^[3]。