- 多元多项式

多元多项式
基本知识
相关知识
设K是一个数域,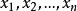 是几个文字(也可称为变量),
是几个文字(也可称为变量),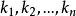 是非负整数,
是非负整数, ,称
,称
![]() 为一个单项式(monomial)。某个指数
为一个单项式(monomial)。某个指数![]() 表示变量
表示变量![]() 不出现,当所有的指数全部等于0时,相应的单项式就是常数项
不出现,当所有的指数全部等于0时,相应的单项式就是常数项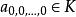 ,
,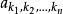 称为此单项式的系数,当
称为此单项式的系数,当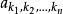 ≠0时,
≠0时,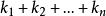 称为此单项式的次数,系数为0的单项式称为零单项式,简记为0,零单项式的次数规定为
称为此单项式的次数,系数为0的单项式称为零单项式,简记为0,零单项式的次数规定为![]() ,为了表示方便,常常把单项式(1)中各个字母的方幂看成一个n维向量
,为了表示方便,常常把单项式(1)中各个字母的方幂看成一个n维向量
![]() 称为这个单项式的指数向量。并把单项式(1)简记为
称为这个单项式的指数向量。并把单项式(1)简记为![]() ,又把向量
,又把向量![]() 的分量之和表为
的分量之和表为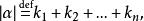 ,于是有(假设
,于是有(假设![]() )
)
![]() 显然指数向量的分量都是非负整数,因此有
显然指数向量的分量都是非负整数,因此有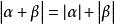 两个单项式:
两个单项式:
![]() 如果满足
如果满足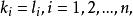 就被称为同类项,也就是说,
就被称为同类项,也就是说,![]() 与
与![]() 是同类项当且仅当它们的指数向量相等,即
是同类项当且仅当它们的指数向量相等,即![]() 。[1]
。[1]
n元多项式的定义
有限多个单项式之和(假设其中不含同类项)
![]() 称为n元多项式,简称多项式,n 元多项式
称为n元多项式,简称多项式,n 元多项式![]() 中非零单项式的最高次数称为多项式
中非零单项式的最高次数称为多项式![]() 的次数,记为
的次数,记为![]() 。只含零单项式的多项式称为零多项式,记为0,零多项式的次数规定为
。只含零单项式的多项式称为零多项式,记为0,零多项式的次数规定为![]() ,例如若
,例如若
![]() 则
则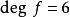 。
。
有很多时候需要把多元多项式看成其中某一个变量,例如![]() 的一元多项式
的一元多项式
![]() 这里的系数
这里的系数 都是多项式环
都是多项式环 中的元素,我们把
中的元素,我们把![]() 作为某个变量
作为某个变量![]() 的一元多项式的次数称为
的一元多项式的次数称为![]() 关于
关于![]() 的次数,记为
的次数,记为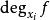 。[1]
。[1]
和一元多项式一样,对于n元多项式也可同样地定义相等、相加、相减和相乘,例如当两个单项式是同类项时,可以通过系数相加而合并成一项:
![]() 两个单项式相乘则是把指数向量相加,再把系数相乘:
两个单项式相乘则是把指数向量相加,再把系数相乘:
![]()
n元多项式的加法和乘法具有与一元多项式相同的性质,因此把数域K上所有以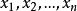 为变量的n元多项式的集合记为
为变量的n元多项式的集合记为
![]() 并称为数域K上的n元多项式环。[1]
并称为数域K上的n元多项式环。[1]
多项式的排序问题
现在我们要研究单项式的排序问题,对于一元多项式,按各个项的次数来排列是最自然的,但是对于多元多项式,有相同次数的项不止一个,单按次数排列具有不确定性,所以有必要采用字典排列法。为此首先在指数向量的集合内定义一个序:对于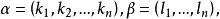 ,如果存在
,如果存在![]() 使得
使得
![]() 则称
则称![]() 优于
优于![]() ,记为
,记为![]() ,例如
,例如
![]() 从这个定义立即可以看出,对于任意两个不相等的指数向量
从这个定义立即可以看出,对于任意两个不相等的指数向量![]() ,不是
,不是![]() 就是
就是![]() ,两者必居其一。而且关系“
,两者必居其一。而且关系“![]() ”还具有传递性,即从
”还具有传递性,即从![]() 与
与![]() 可以得出
可以得出![]() ,这说明“
,这说明“![]() ”确实是指数向量集合的一个序,利用指数向量的序就可以定义单项式的序,即
”确实是指数向量集合的一个序,利用指数向量的序就可以定义单项式的序,即
![]() 我们把这个序(包括指数向量的序以及单项式的序)称为字典序(lexicographicorder)。这样就可以把多项式中的项按字典序排列,当n=1时这种排列法就是降幂排列法,多项式中按字典排列法次序最前的非零项称为此多项式的首项。[1]
我们把这个序(包括指数向量的序以及单项式的序)称为字典序(lexicographicorder)。这样就可以把多项式中的项按字典序排列,当n=1时这种排列法就是降幂排列法,多项式中按字典排列法次序最前的非零项称为此多项式的首项。[1]
相关性质
字典排列法的首项有以下性质。
定理1
两个非零多项式的乘积的首项等于这两个多项式的首项的乘积。
证明:设这两个多项式是![]() ,它们的乘积是
,它们的乘积是![]() .设
.设![]() 的首项分别为
的首项分别为
![]() 它们的乘积等于
它们的乘积等于
![]() 乘积多项式h中的任意单项式的指数向量具有
乘积多项式h中的任意单项式的指数向量具有![]() 的形式,其中,
的形式,其中,![]() 分别是
分别是![]() 中的单项式的指数向量,因此有
中的单项式的指数向量,因此有
![]() 我们要证
我们要证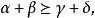 ,并且等号成立当且仅当
,并且等号成立当且仅当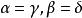 。首先设
。首先设![]() 若
若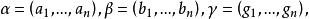 ,则一定存在i≤n使得
,则一定存在i≤n使得
![]() 于是
于是
![]() 即
即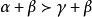 。同理当
。同理当![]() 时有
时有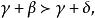 因此
因此
![]() 而且只要
而且只要![]() 或
或![]() 有一个成立,就有
有一个成立,就有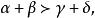 这说明(2)式确是h的首项而且h中没有同类项会和它相消。[1]
这说明(2)式确是h的首项而且h中没有同类项会和它相消。[1]
推论2
两个非零多项式的乘积仍是非零多项式。[1]

-
将于3月24日上市 整车多项升级/搭载双激光雷达
2025-10-31 04:47:26 查看详情 -
小鹏全新P7i将于今日上市 整车多项升级/搭载双激光雷达
2025-10-31 04:47:26 查看详情 -
上海车展上市 整车多项升级/搭载双激光雷达
2025-10-31 04:47:26 查看详情 -
奥迪新款A6L正式上市 多项服务政策加持
2025-10-31 04:47:26 查看详情 -
长城炮引领多元生活方式 试驾长城炮越野皮卡
2025-10-31 04:47:26 查看详情 -
长城炮引领多元生活方式 评测长城哈弗H9中大型SUV怎么样
2025-10-31 04:47:26 查看详情 -
长城炮乘用皮卡全球版 长城炮引领多元生活方式
2025-10-31 04:47:26 查看详情 -
长城造 长城炮引领多元生活方式
2025-10-31 04:47:26 查看详情 -
长城炮引领多元生活方式 成都长城哈弗H6现车充足
2025-10-31 04:47:26 查看详情 -
长城炮给出答案 长城炮引领多元生活方式
2025-10-31 04:47:26 查看详情


 求购
求购

