- 边边角

边边角
质疑
主要问题:条件(两个三角形都分别为边边直角、边边钝角、边边锐角时),这样的说法包含了边边角的所有形式,所以错误。
修改
命题部分
“边边锐角是全等三角形‘应该改为’锐角三角形的边边角对应相等为全等”,或者说“两条边对应角为锐角的三角形边边角对应相等为全等”。
也就是说两条边的夹角可能是钝角(此时不成立)。
正文部分
钝角三角形的边边角对应相等为全等三角形的定义不成立。(见下图)
条件1:△ABC和△A’B’C’两个三角形都为钝角三角形(钝角三角形)
条件2:AB=A’B’,AC=A’C’,∠B=∠B’。(边边角)
判断:以上条件还不能确定两个三角形为全等三角形(不成立)
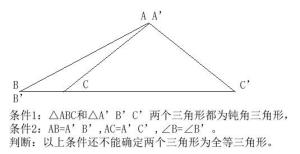
应更改为:
假命题。
如两个三角形都分别为边边直角、边边钝角,这种情况成立,或者说三角形是直角三角形、钝角三角形时的边边角对应相等时,情况也成立。
但条件为边边锐角时,分别有钝角-边-锐角-边-锐角、锐角-边-锐角-边-锐角、锐角-边-钝角-边-锐角几种情况,所以只是边边锐角对应相等的条件不能证明其为全等三角形。(见下图)
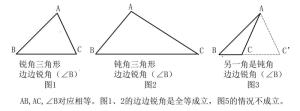
证明
都是直角三角形的情况
【在数学选择题中SSA的证明是错误的】
解:已知:∠A=∠D=90°,AC=DF,AB=DE,∠B=∠E。
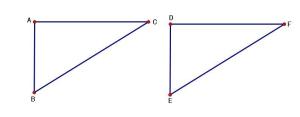 1求证:△ABC≌△DEF证明:在△ABC和△DEF中:
1求证:△ABC≌△DEF证明:在△ABC和△DEF中:
【AC=DF】
【AB=DE】
【∠A=∠D】
∴△ABC≌△DEF(SAS)
都是锐角三角形的情况
解:已知:AB=A'B',AC=A'C',∠B=∠B'。
求证:△ABC≌△A'B'C'。
证明:过点A作垂线交BC于D。(另一幅图同,不写)
∵AD⊥BC,A'D'⊥B'C'
 2∴∠ADC=∠A'D'C'=90°在△ABD和△A'B'D'中:
2∴∠ADC=∠A'D'C'=90°在△ABD和△A'B'D'中:
【∠B=∠B'】
【∠ADB=∠A'D'B'】
【AB=A'B'】
∴△ABD≌△A'B'D'(AAS)
∴BD=B'D',AD=A'D'
∵AD⊥BC,A'D'⊥B'C'
∴∠ADC=∠A'D'C'=90°
在Rt△ADC和Rt△A'D'C'中:
【AD=A'D'】
【AC=A'C'】
∴Rt△ADC≌Rt△A'D'C'(HL)
∴DC=D'C'
∴BD+B'D'=DC+D'C'
即BC=B'C'
在△ABC和△A'B'C'中:
【AB=A'B'】
【AC=A'C'】
【BC=B'C'】
∴△ABC≌△A'B'C'(SSS)
结论
如果两个三角形均为直角三角形、锐角三角形,又符合有“在两个三角形中,两条边和其中一边的对角分别对应相等”的情况,那么这两个三角形全等。



 求购
求购




