- 反馈网络

反馈网络
概念
定义
反馈网络(Recurrent Network),又称自联想记忆网络,其目的是为了设计一个网络,储存一组平衡点,使得当给网络一组初始值时,网络通过自行运行而最终收敛到这个设计的平衡点上。
1982年,物理学家霍普菲尔德(J.Hopfield)发表了一篇对人工神经网络研究颇有影响的论文。
反馈网络能够表现出非线性动力学系统的动态特性。它所具有的主要特性为以下两点:
第一、网络系统具有若干个稳定状态。当网络从某一初始状态开始运动,网络系统总可以收敛到某一个稳定的平衡状态;
第二,系统稳定的平衡状态可以通过设计网络的权值而被存储到网络中。
网络结构形式
Hopfield网络是单层对称全反馈网络,根据激活函数选取的不同,可分为离散型和连续性两种(DHNN,CHNN)。
DHNN:激活函数f(·)是一个二值型的硬函数,即ai=sgn(ni),i=l, 2, … r,主要用于联想记忆;
CHNN: 激活函数f(·)为一个连续单调上升的有界函数,主要用于优化计算。
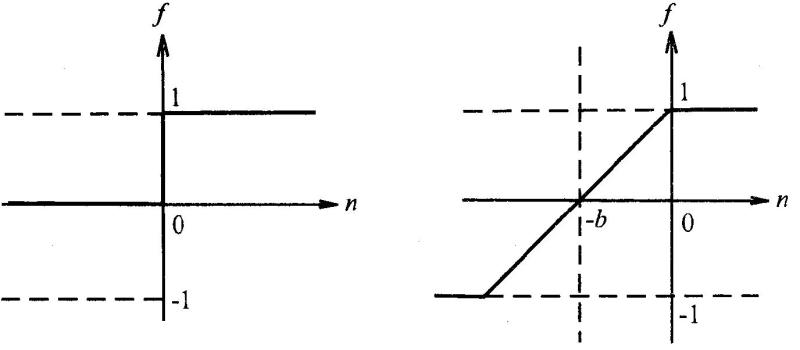 图1
图1
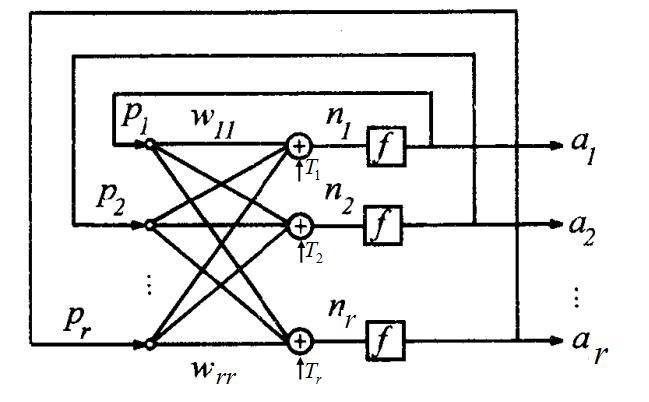 图2
图2
工作原理
非线性系统状态演变的形式
设状态矢量N=[n1, n2, …,nr],网络的输出矢量为A=[a1,a2…,ar] ,
在一个r维状态空间上,可以用一条轨迹来描述状态变化情况。
从初始值N(t0)出发, N(t0+Δt)→N(t0+2Δt)→…→N(t0+mΔt),这些在空间上的点组成的确定轨迹,是演化过程中所有可能状态的集合,我们称这个状态空间为相空间。
对于DHNN,因为N(t)中每个值只可能为±1,或{0,1},对于确定的权值wij,其轨迹是跳跃的阶梯式,如图中A所示。
对于CHNN,因为f(·)是连续的,因而,其轨迹也是连续的。如图3的B、C所示。
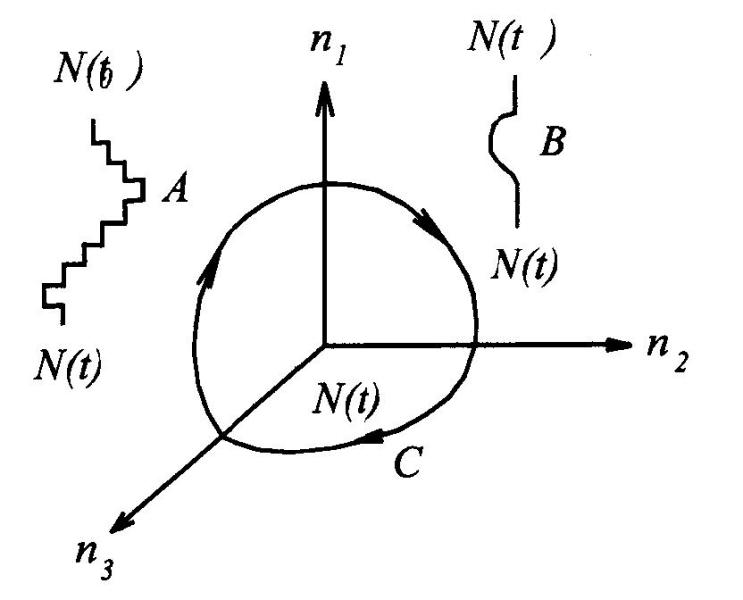 图3
图3
在Hopfield网络中,由于反馈的存在,对于不同的连接权值wij和输入Pj(i, j=1, 2, … r),反馈网络状态轨迹可能出现以下几种情况:(1)渐进稳定;(2)极限环;(3)混沌现象;(4)状态轨迹发散;
(1)状态轨迹为稳定点
状态轨迹从系统在t0时状态的初值N(t0)开始,经过一定的时间t(t>0)后,到达N(t0+t)。如果N(t0+t+Δt)=N(t0+t),Δt>0,则状态N(t0+t)称为网络的稳定点,或平衡点。
即反馈网络从任一初始态P(0)开始运动,若存在某一有限时刻t,从t以后的网络状态不再发生变化:P(t+Δt)= P(t),Δt>0,则称该网络是稳定的。
处于稳定时的网络状态叫做稳定状态,又称为定吸引子。
在一个反馈网络中,存在很多稳定点,根据不同情况,这些稳定点可以分为:
1)渐近稳定点:如果在稳定点Ne周围的N(σ)区域内,从任一个初始状态N(t0)出发的每个运动,当t→∞时都收敛于Ne,则称Ne为渐近稳定点。
2)不稳定平衡点Nen:在某些特定的轨迹演化过程中,网络能够到达稳定点Nen,但对于其它方向上的任意一个小的区域N(σ),不管N(σ)取多么小,其轨迹在时间t以后总是偏离Nen;
3)网络的解:如果网络最后稳定到设计人员期望的稳定点,且该稳定点又是渐近稳定点,那么这个点称为网络的解;
4)网络的伪稳定点:网络最终稳定到一个渐近稳定点上,但这个稳定点不是网络设计所要求的解,这个稳定点为伪稳定点。
(2)状态轨迹为极限环
如果在某些参数的情况下,状态N(t)的轨迹是一个圆,或一个环,状态N(t)沿着环重复旋转,永不停止,此时的输出A(t)也出现周期变化,即出现振荡,如图6.4中C的轨迹即是极限环出现的情形。
对于DHNN,轨迹变化可能在两种状态下来回跳动,其极限环为2。如果在r种状态下循环变化,称其极限环为r。
(3)混沌现象
如果状态N(t)的轨迹在某个确定的范围内运动,但既不重复,又不能停下来,状态变化为无穷多个,而轨迹也不能发散到无穷远,这种现象称为混沌(chaos)。
在出现混沌的情况下,系统输出变化为无穷多个,并且随时间推移不能趋向稳定,但又不发散。
(4) 状态轨迹发散
如果状态N(t)的轨迹随时间一直延伸到无穷远,此时状态发散,系统的输出也发散。
在人工神经网络中,由于输入、输出激活函数上一个有界函数,虽然状态N(t)是发散的,但其输出A(t)还是稳定的,而A(t)的稳定反过来又限制了状态的发散。
一般非线性人工神经网络中发散现象是不会发生的,除非神经元的输入输出激活函数是线性的。
Hopfield网络的稳定性可用能量函数进行分析。人工神经网络常利用渐进稳定点来解决某些问题。例如,如果把系统的稳定点视为一个记忆的话,那么从初态朝这个稳定点的演变过程就是寻找记忆的过程。初态可以认为是给定的有关记忆的部分信息。如果把系统的稳定点视为一个能量函数的极小点,把能量函数视为一个优化问题的目标函数,那么从初态朝这个稳定点的演变过程就是一个求该优化问题的过程。这样的优点在于它的解并不需要真的去计算,而只要构成这种反馈网络,适当的设计其连接值和输入就可达到目的。
离散型的Hopfield神经网络
网络结构及I/O关系
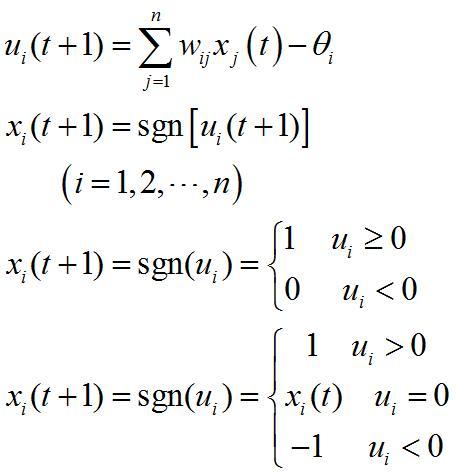 图4
图4
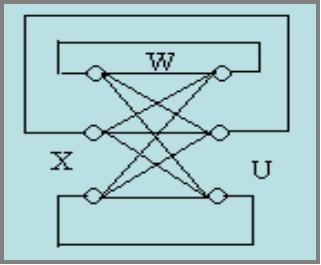 图5
图5
两种工作方式
DHNN主要有以下两种工作方式:
(1)串行工作方式 在某一时刻只有一个神经元按照上式改变状态,而其它神经元的输出不变。这一变化的神经元可以按照随机的方式或预定的顺序来选择。
这种更新方式的特点是:
实现上容易,每个神经元有自己的状态更新时刻,不需要同步机制; 功能上的串行状态更新可以限制网络的输出状态,避免不同稳态等概率的出现;
异步状态更新更接近实际的生物神经系统的表现。
(2)并行工作方式 在某一时刻有N个神经元按照上式改变状态,而其它的神经元的输出不变。变化的这一组神经元可以按照随机方式或某种规则来选择。当N=n时,称为全并行方式。对于权值设计要求较高。
DHNN的稳定性与吸引子
网络达到稳定时的状态,称为网络的吸引子。非线性系统的稳定点。
Hopfield网络自提出后,被认为是一种最典型的全反馈网络,可以看作一种非线性的动力学系统 。 网络状态的变化,是一种在超立方体中的自由运动状态,1892年, Lyapunov(李雅普诺夫)提出了关于稳定性概念的基本理论,并被称为Lyapunov定理。
关于吸引子的吸引域:
1,弱吸引域定义:若Xa是吸引子,对于异步方式,若存在一个调整次序,使网络可以从状态X演变到Xa,则称X弱吸引到Xa;若有某些X弱吸引到Xa ,则称这些X的集合为Xa的弱吸引域。
2,强吸引域定义:若Xa是吸引子,对于任意调整次序,网络都可以从状态X演变到Xa,则称X强吸引到Xa;若有某些X强吸引到Xa ,则称这些X的集合为Xa的强吸引域。
吸引子的数量代表联想网络的记忆容量。是指网络在一定的联想出错概率容许下,存储互不干扰的吸引子的数量。
吸引子的数量与吸引域有关,吸引域大的网络联想能力强,容错性好,但吸引子的数量就受到限制。
DHNN网络设计
吸引子的分布是由网络的权值和阈值决定的,设计吸引子的核心就是如何设计一组合适的权值。为了使设计的权值满足要求,权值矩阵应符合下述要求:
(1)为了保证异步方式工作时网络收敛,W应为对称阵;
(2)为了保证同步工作方式时网络收敛,W应为非负定对称阵;
(3)保证给定的样本是网络的吸引子,并且要有一定的吸引域。
连续性的Hopfield网络
CHNN是在DHNN的基础上提出的,它的原理和DHNN相似。由于CHNN是以模拟量作为网络的输入输出量,各神经元采用并行方式工作,所以它在信息处理的并行性、联想性、实时性、分布存储、协同性等方面比DHNN更接近于生物神经网络。我们将从以下几点来讨论CHNN。
1、网络模型
2、CHNN方程的解及稳定性分析
3、关于Hopfield能量函数的几点说明
4、关于CHNN的几点结论
网络模型
 图6
图6
 图7
图7
CHNN方程的解及稳定性分析
 图8
图8
关于Hopfield能量函数的 几点说明
当对反馈网络应用能量函数后,从任一初始状态开始,因为在每次迭代后都能满足E≤0,所以网络的能量将会越来越小,最后趋于稳定点E=0。
Hopfield能量函数的物理意义是:在那些渐进稳定点的吸引域内,离吸引点越远的状态,所具有的能量越大,由于能量函数的单调下降特性,保证状态的运动方向能从远离吸引点处,不断地趋于吸引点,直到达到稳定点。
几点说明:
1)能量函数为反馈网络的重要概念。根据能量函数可以方便的判断系统的稳定性;
2)能量函数与李雅普诺夫函数的区别在于:李氏被限定在大于零的范围内,且要求在零点值为零;
3)Hopfield选择的能量函数,只是保证系统稳定和渐进稳定的充分条件,而不是必要条件,其能量函数也不是唯一的。
关于CHNN的几点结论
1)具有良好的收敛性;
2)具有有限个平衡点;
3)如果平衡点是稳定的,那么它也一定是渐进稳定的;
4)渐进稳定平衡点为其能量函数的局部极小点;
5)能将任意一组希望存储的正交化矢量综合为网络的渐进平衡点;
6)网络以大规模、非线性、连续时间并行方式处理信息,其计算时间就是网络趋于平衡点的时间。[1]

-
第十八届中国网络媒体论坛
2025-09-20 22:19:48 查看详情 -
北京大学网络教育学院
2025-09-20 22:19:48 查看详情 -
2018中国网络媒体论坛共识
2025-09-20 22:19:48 查看详情 -
网络表演经营活动管理办法
2025-09-20 22:19:48 查看详情 -
网络直播平台管理规范
2025-09-20 22:19:48 查看详情


 求购
求购







