- 积分学

积分学
学科概念
 积分学数学分析中的积分指的是一元和多元实函数在黎曼意义下的积分。各类积分中最基 本的是定积分和作为微分逆运算并为计算定积分服 务的不定积分,其他的还有重积分、曲线积分、曲面 积分和各种情形下的反常积分。这些都是定积分的推广。
积分学数学分析中的积分指的是一元和多元实函数在黎曼意义下的积分。各类积分中最基 本的是定积分和作为微分逆运算并为计算定积分服 务的不定积分,其他的还有重积分、曲线积分、曲面 积分和各种情形下的反常积分。这些都是定积分的推广。
研究积分(包括定积分与不定积分)的性质、计算方法与应用的一个微积分学分支。积分学的出现,比微分学早得多,在古希腊数学中,已有积分思想的萌芽。
开普勒、卡瓦莱利、费马、瓦里斯、帕斯卡等人,为积分学的形成奠定了基础。
在1696年,约翰·伯努利把这门学科定名为“积分学”,取代以前由莱布尼兹命名的“求和学”。
学科发展
积分这个词是雅各布第一 ·伯努利(Bemoul一 li,Jacob I )于1690年首先使用的。
1696年,莱布尼茨(Leibniz,G. W.)与他确定用积分学这个词代替 莱布尼茨原来使用的求和计算这个名称。积分学源于求曲线形的面积、弧长和立体体积等几何问题,以及由变速运动物体的速度求它经过的路程的力学问 题。它的思想萌芽可追溯到古希腊时期用以求面积和体积的穷竭法。莱布尼茨实质上接受了卡瓦列里 (Cavalieri,(F.)B.)不可分量法的思想,将图形看成 无穷多个宽度为无穷小的矩形之和。
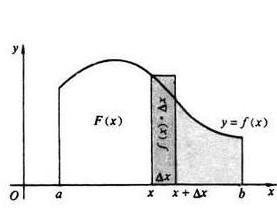
牛顿(Newton,I.)从另一途径导致积分概念.他首先确定曲线下的面积*5对曲线的横坐 标^的变化率(即导数)为纵坐标 >这样面积S就 可以由3<经过反微分得出.在本例中曲线是y =
莱布尼茨的积分是无穷多个无穷小之和,牛顿的积分则是反 微分。两人又几乎同时互相独立地得出积分与微分的互逆关系(前者在1675年,后者在1666年),由此得到在很多情况下可行的积分计算方法,即通过求 原函数算积分,这样积分才成为真正有意义的概念,它也标志着积分学这个新学科的创立。
理论表现
积分学的理论表现在两个主要方面: 函数的积分与集合的测度。
集合的测度理论起源于欧多克斯与阿基米德的工作中. 由康托与若当进行了推广. 随着波雷尔,勒贝格及卡拉西奥多里的研究成果,它有了现在的形式。
函数积分的理论是随帕斯卡,费马,莱布尼茨及欧拉的工作开始的. 柯西与黎曼加以精确化并推广了它.以后随勒贝格,拉东及黎兹的工作,使它有了现在的形式。
由丹尼尔引入的测度一般理论使上述两个方面统一了起来。
积分理论与原函数理论之间的联系由勒贝格,斯蒂尔吉斯及当儒瓦进行了研究。
测度论与概率论之间的联系由波雷尔,辛钦,柯尔莫哥罗夫给出。



 求购
求购








