- 摆线

摆线
别称
一个圆在一条定直线上滚动时,圆周上一个定点的轨迹,又称圆滚线、旋轮线。
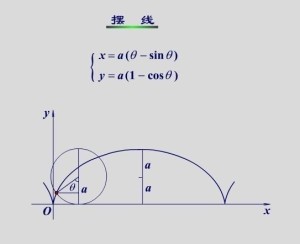
 摆线圆上定点的初始位置为坐标原点,定直线为x轴。当圆滚动j 角以后,圆上定点从 O 点位置到达P点位置。当圆滚动一周,即 j从O变动2π时,动圆上定点描画出摆线的第一拱。再向前滚动一周, 动圆上定点描画出第二拱,继续滚动,可得第三拱,第四拱……,所有这些拱的形状都是完全相同的 ,每一拱的拱高为2a(即圆的直径),拱宽为2πa(即圆的周长)。
摆线圆上定点的初始位置为坐标原点,定直线为x轴。当圆滚动j 角以后,圆上定点从 O 点位置到达P点位置。当圆滚动一周,即 j从O变动2π时,动圆上定点描画出摆线的第一拱。再向前滚动一周, 动圆上定点描画出第二拱,继续滚动,可得第三拱,第四拱……,所有这些拱的形状都是完全相同的 ,每一拱的拱高为2a(即圆的直径),拱宽为2πa(即圆的周长)。
性质
到17 世纪,人们发现摆线具有如下性质:
1.它的长度等于旋转圆直径的 4 倍。尤为令人感兴趣的是,它的长度是 一个不依赖于π的有理数。
2.在弧线下的面积,是旋转圆面积的三倍。
 摆线3.圆上描出摆线的那个点,具有不同的速度——事实上,在特定的地方它甚至是静止的。
摆线3.圆上描出摆线的那个点,具有不同的速度——事实上,在特定的地方它甚至是静止的。
4.当弹子从一个摆线形状的容器的不同点放开时,它们会同时到达底部。
方程式
 摆线x=r*(t-sint); y=r*(1-cost)r为圆的半径, t是圆的半径所经过的弧度(滚动角),当t由0变到2π时,动点就画出了摆线的一支,称为一拱。
摆线x=r*(t-sint); y=r*(1-cost)r为圆的半径, t是圆的半径所经过的弧度(滚动角),当t由0变到2π时,动点就画出了摆线的一支,称为一拱。
历史
摆线最早出现可见于公元 1501 年出版的 C·鲍威尔的一本书中.但在 17 世 纪,大批卓越的数学家(如伽利略,帕斯卡,托里拆利,笛卡儿,费尔马, 伍任,瓦里斯,惠更斯,约翰·伯努利,莱布尼兹,牛顿等等)热心于研究这一曲线的性质.17 世纪是人们对数学力学和数学运动学爱好的年代,这能解释人们为什么对摆线怀有强烈的兴趣。在这一时期,伴随着许多发现,也出现了众多有关发现权的争议,剽窃的指责,以及抹煞他人工作的现象。这样,作为一种结果,摆线被贴上了引发争议的“金苹果”和“几何的海伦” 的标签。
摆线的研究最初开始于库萨的尼古拉,之后马兰·梅森也有针对摆线的研究。1599年伽利略为摆线命名。1634年吉勒斯·德·罗贝瓦勒指出摆线下方的面积是生成它的圆面积的三倍。1658年克里斯多佛·雷恩也向人们指出摆线的长度是生成它的圆直径的四倍。在这一时期,伴随着许多发现,也出现了众多有关发现权的争议,甚至抹杀他人工作的现象,而因此摆线也被人们称作“几何学中的海伦”(The Helen of Geometers)。[2]
相关故事
时钟
时钟已变成现代人不可或少的必备工具之一,没有时钟,人们将不知时间,许多重要的约会便会错过,当各位在看表的时候,不知可曾想过,时钟里面隐藏了些甚么道理,一砂一世界,许多我们视为理所当然的事都是先民流血流汗一点一滴累积而成的。
在时钟里面到底隐藏了什么东西 将这些理论写出来可是厚厚的一大本呢!回想以前的中世纪航海时代,时间的掌握是关乎全船人生命安危的大事,想要和大海搏斗,时间是不可或缺的因素,古时候是以沙漏水钟来计时,但这些计时工具相当不准确,为了增加船员生存的机会,发明精确的计时器变成了当时科学界的当务之急。
那时在意大利有一位年轻的科学家伽利略,有一次在比萨斜塔处意外地发现一个有趣的现象,教堂的吊灯来回摆动时,不管摆动的幅度大还是小,每摆动一次用的时间都相等。当时,他是以自己的心跳脉搏来计算时间的.从此以后,伽利略便废寝忘食的研究起物理和数学来,他曾用自行制的滴漏来重新做单摆的试验,结果证明了单摆摆动的时间跟摆幅没有关系,只跟单摆摆线的长度有关.这个现象使伽利略想到或许可以利用单摆来制作精确的时钟,但他始终并没有将理想付之实行。
伽利略的发现振奋了科学界,可是不久便发现单摆的摆动周期也不完全相等。原来,伽利略的观察和实验还不够精确.实际上,摆的摆幅愈大,摆动周期就愈长,只不过这种周期的变化是很小的。所以,如果用这种摆来制作时钟,摆的振幅会因为摩擦和空气阻力而愈来愈小,时钟也因此愈走愈快。
过了不久,荷兰科学家惠更斯决定要做出一个精确的时钟来.伽利略的单摆是在一段圆弧上摆动的,所以我们也叫做圆周摆。惠更斯想要找出一条曲线,使摆沿著这样的曲线摆动时,摆动周期完全与摆幅无关,这群科学家放弃了物理实验,纯粹往数学曲线上去研究,经过不少次的失败,这样的曲线终於找到了,数学上把这种曲线叫做“摆线”,“等时曲线”或“旋轮线”。
动手验证
如果你用硬纸板剪一个圆,在圆的边缘固定一枝铅笔,当这圆沿一条直线滚动时,铅笔便会画出一条摆线来.相信这样的玩具许多人都已经看过玩过,以前的街上,常会看到街边小贩在兜售这种摆线玩具,许多人赞叹摆线的美丽,但却不知摆线与时钟的相关性.钟表店里面那些有钟摆的时钟,都是利用摆线性质制作出来的.由于摆线的发现,使得精确时钟的制作不是梦想.这也使人类科技向前迈进一大步。
基本原理
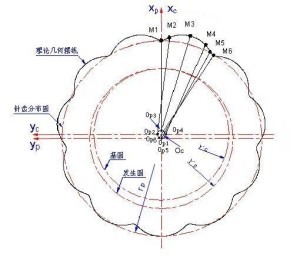
摆线针轮行星传动中,摆线轮齿廓曲线运用内啮合发生圆产生的短幅外摆线。[1]
有一发生圆(滚圆)半径为rp',基圆半径为rc',基圆内切于发生圆,当发生圆绕基圆作纯滚动,其圆心Op分别处于Op1、Op2、Op3、Op4、Op5、Op6......各位置时,由此固结在发生圆平面上的点M分别经过M1、M2、M3、M4、M5、M6......各位置,由此发生圆周期滚动,发生圆上点M所形成的轨迹曲线即为短幅外摆线。
由以上摆线生成的几何关系 若仍保持以上的内切滚动关系,将基圆和摆线视为刚体相对于发生圆运动,则形成了摆线图形相对发生圆圆心Op作行星方式的运动,这就是行星摆线传动机构的基本原理。
最速降线
在一个斜面上,摆两条轨道,一条是直线,一条是曲线,起点高度以及终点高度都相同。两个质量、大小一样的小球同时从起点向下滑落,曲线的小球反而先到终点。这是由于曲线轨道上的小球先达到最高速度,所以先到达。然而,两点之间的直线只有一条,曲线却有无数条,那么,哪一条才是最快的呢?伽利略于1630年提出了这个问题,当时他认为这条线应该是一条弧线,可是后来人们发现这个答案是错误的。1696年,瑞士数学家约翰·伯努利解决了这个问题,他还拿这个问题向其他数学家提出了公开挑战。牛顿、莱布尼兹、洛比达以及雅克布·伯努利等解决了这个问题。这条最速降线就是一条摆线,也叫旋轮线。
意大利科学家伽利略在1630年提出一个分析学的基本问题——“一个质点在重力作用下,从一个给定点到不在它垂直下方的另一点,如果不计摩擦力,问沿着什么曲线滑下所需时间最短。”。他说这曲线是圆,可是这是一个错误的答案。
瑞士数学家约翰.伯努利在1696年再提出这个最速降线的问题(problem of brachistochrone),征求解答。次年已有多位数学家得到正确答案,其中包括牛顿、莱布尼兹、洛必达和伯努利家族的成员。这问题的正确答案是连接两个点上凹的唯一一段旋轮线。
旋轮线与1673年荷兰科学家惠更斯讨论的摆线相同。因为钟表摆锤作一次完全摆动所用的时间相等,所以摆线(旋轮线)又称等时曲线。
看Johann Bernoulli 对最速降线问题的beautiful解答:
如果使分成的层数n无限地增加,即每层的厚度无限地变薄,则质点的运动便趋于空间A、B两点间质点运动的真实情况,此时折线也就无限增多,其形状就趋近我们所要求的曲线——最速降线.而折线的每一段趋向于曲线的切线,因而得出最速降线的一个重要性质:任意一点上切线和铅垂线所成的角度的正弦与该点落下的高度的平方根的比是常数.而具有这种性质的曲线就是摆线.所谓摆线,它是一个圆沿着一条直线滚动(无滑动)时,圆周上任意一点的轨迹。
因此,最速降线就是摆线,只不过在最速降线问题中,这条摆线是上、下颠倒过来的罢了.
以上便是Johann Bernoulli当时所给最速降线问题的解答.当然,这个解答在理论上并不算十分严谨的.但是,这个解答所蕴含的基本观点的发展,导致了一门新的学科——变分学.最速降线问题的最终而完备的解答,需要用到变分学的知识.
证明式
过原点半径为r的摆线参数方程为

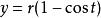
在这里实参数t是在弧度制下,圆滚动的角度。对每一个给出的t,圆心的坐标为(rt, r)。 通过替换解出t可以求的笛卡尔坐标方程为
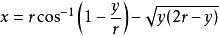
摆线的第一道拱由参数t在(0, 2π)区间内的点组成。
摆线也满足下面的微分方程。
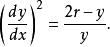
面积
一条由半径为r的圆所生成的拱形面积可以由下面的参数方程界定:[3]
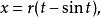
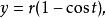
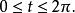
微分,

于是可以求得
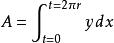
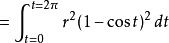
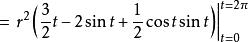
![]()
弧长
弧形的长度可以由下面的式子计算出:[3]
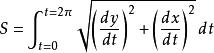
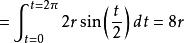

-
9000系列摆线针轮减速机
2025-09-20 10:27:12 查看详情


 求购
求购






