- 显函数

显函数
定义
定义1
对于一个函数,如果已知自变量取某一值时,可以不必通过解方程即能求得因变量的对应值,这样的函数叫做显函数。[1]或者说若y是x的函数,当直接给出y等于一个只含自变量和中间变量的解析式子时,此时y叫做自变量x的显函数。[2]
参考定义2
显函数:一个函数如果能用形如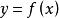 的解析式表示,其中
的解析式表示,其中![]() 分别是函数的自变量与因变量,则此函数称为显函数,如
分别是函数的自变量与因变量,则此函数称为显函数,如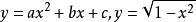 等都是显函数。
等都是显函数。
隐函数:如果由方程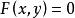 可确定y是x的函数,即
可确定y是x的函数,即![]() 在某个范围内存在函数
在某个范围内存在函数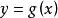 ,使
,使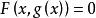 ,由这种方式表示的函数是隐函数。[3]
,由这种方式表示的函数是隐函数。[3]
参考定义3
显函数:自变量与因变量已经明显分离的函数称为“显函数”,如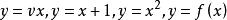 等都是显函数。
等都是显函数。
隐函数:自变量与因变量没有明显分离或无法分离的函数称为“隐函数”(意思是这种函数的函数关系“隐藏”在方程之中),如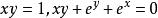 等都是隐函数,一元隐函数的一般形式是
等都是隐函数,一元隐函数的一般形式是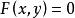 。[4]
。[4]
隐函数与显函数的区别
如果方程f(x,y)=0能确定y与x的对应关系,那么称这种表示方法表示的函数为隐函数。 隐函数不一定能写为y=f(x)的形式,如x2+y2=0。因此按照函数"设x和y是两个变量,D是实数集的某个子集,若对于D中的每个值,变量x按照一定的法则有一个确定的值y与之对应,称变量y为变量x的(显)函数,记作 y=f(x)"的定义,隐函数不一定是“函数”,而是“方程”。 也就是说,函数都是方程,但方程却不一定是函数。显函数是用y=f(x)表示的函数,左边是一个y右边是x的表达式 比如y=2x+1。隐函数是x和y都混在一起的,比如2x-y+1=0。有些隐函数可以表示成显函数,叫做隐函数显化,但也有些隐函数是不能显化的,比如ey+xy=1。
显函数与隐函数的区别不是绝对的。有些隐函数可以化成显函数,如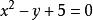 (R为常数)可以化成
(R为常数)可以化成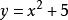 ;有些隐函数如
;有些隐函数如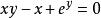 虽然也确定著x,y之间的函数关系,但y不能化为x的显函数。
虽然也确定著x,y之间的函数关系,但y不能化为x的显函数。
显函数求导
若可导函数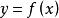 的导函数
的导函数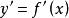 仍然可导,则称
仍然可导,则称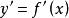 的导数为函数
的导数为函数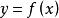 的二阶导数,记作
的二阶导数,记作![]() ,或
,或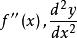 ,即
,即
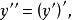 或
或
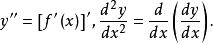 相应地,称
相应地,称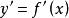 为函数
为函数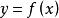 的一阶导数。
的一阶导数。
类似地,若![]() 仍然可导,则称
仍然可导,则称![]() 的导数
的导数 为函数
为函数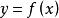 的三阶导数,记作
的三阶导数,记作![]() ,或
,或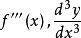 。
。
一般地,若函数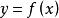 的n-1阶导函数仍然可导,则称n-1阶导函数的导数为函数
的n-1阶导函数仍然可导,则称n-1阶导函数的导数为函数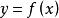 的n阶导数,记作
的n阶导数,记作![]() .或
.或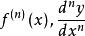 ,即
,即
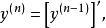 或
或

函数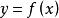 在点
在点![]() 处的n阶导数值记作
处的n阶导数值记作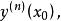 或
或 。
。
函数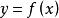 的二阶及二阶以上的导数统称为函数
的二阶及二阶以上的导数统称为函数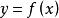 的高阶导数。[5]
的高阶导数。[5]

-
1641函数信号发生器
2025-11-03 03:15:28 查看详情 -
新款荣威550 荣威550仪表显制动力不足是怎么回事
2025-11-03 03:15:28 查看详情


 求购
求购









