- 立方和公式

立方和公式
公式
立方和公式
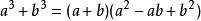
立方差公式
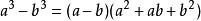
三项立方和公式

推导过程
立方和:
a³+b³
=a³+a²b-a²b+b³
=a²(a+b)-b(a²-b²)
=a²(a+b)-b(a+b)(a-b)
=(a+b)[a²-b(a-b)]
=(a+b)(a²-ab+b²)
立方差:
a3-b3
=a3-b3+a2b-a2b
=a2(a-b)+b(a2-b2)
=a2(a-b)+b(a+b)(a-b)
=[a2+b(a+b)](a-b)
=(a-b)(a2+ab+b2)
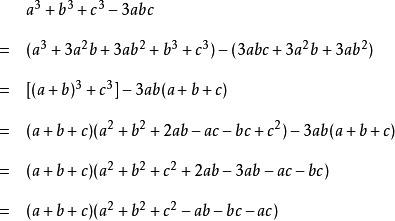
完全立方公式
(a-b)³=a³+3ab²-3a²b-b³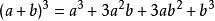
分解步骤如下
(a+b)3=(a+b)(a+b)(a+b) = (a2+2ab+b2)(a+b)=a3+3a2b + 3ab2+ b3
解题时常用它的变形
(a+b)3= a3+ b3+ 3ab(a+b) 和 a3+ b3= (a+b)3- 3ab(a+b)
(a-b)³=(a-b)(a-b)(a-b)=(a²-2ab+b²)(a-b)=a³-3a²b+3ab²-b³
立方和累加
正整数范围中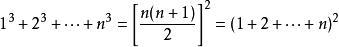
注:可用数学归纳法证明
公式证明
迭代法一
我们知道:
0次方和的求和公式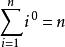 ,即
,即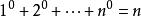
1次方和的求和公式 ,即
,即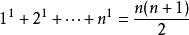
2次方和的求和公式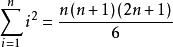 ,即
,即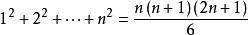 ——平方和公式,此公式可由同种方法得出,取公式
——平方和公式,此公式可由同种方法得出,取公式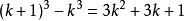 ,迭代即得[2]。
,迭代即得[2]。
具体如下:
(k+1)3- k3= (k3+ 3k2+ 3k + 1) - k3= 3k2+ 3k + 1
利用上面这个式子有:
23- 13= 3×12+ 3×1 + 1
33- 23= 3×22+ 3×2 + 1
43- 33= 3×32+ 3×3+ 1
53- 43= 3×42+ 3×4 + 1
……
(n+1)3- n3= 3×n2+ 3n + 1
把上述各等式左右分别相加 得到:
(n+1)3-13= 3×(12+22+32+……+n2) + 3×(1+2+3+……+n)+n×1
n3+ 3n2+ 3n + 1 - 1 = 3×(12+22+32+……+n2)+3×n(n+1)/2+n (1)
其中12+ 22+ 32+ …… + n2= n(n+1)(2n+1)/6
代入(1)式,整理後得 13+ 23+ 33+ …… + n3=[n(n+1)/2]2
迭代法二
取公式: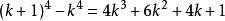
系数可由杨辉三角形来确定
那么就得出:
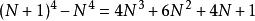 …………⑴
…………⑴
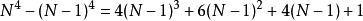 …………⑵
…………⑵
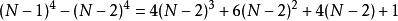 …………⑶
…………⑶
…………
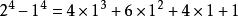 …………(n).
…………(n).
于是⑴+⑵+⑶+…+(n)有
左边=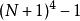
右边=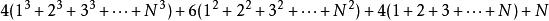
把以上这已经证得的三个公式代入,
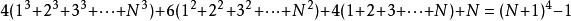
得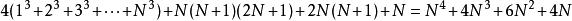
移项后得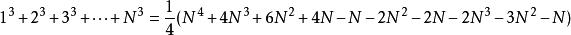
等号右侧合并同类项后得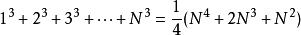
即
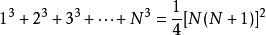
推导完毕。
排列组合法
设数列{![]() }=n(n+1)(n+2),其n项和为
}=n(n+1)(n+2),其n项和为![]() ,且设
,且设![]() =
=![]() +
+![]() +
+![]() +…+
+…+![]() ,则
,则
![]() =1×(1+1)×(1+2)+2×(2+1)×(2+2)+…+n(n+1)(n+2)
=1×(1+1)×(1+2)+2×(2+1)×(2+2)+…+n(n+1)(n+2)
=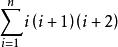
=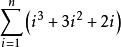
=![]() +3
+3![]() +2
+2![]()
=![]() +3×
+3×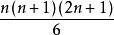 +2×
+2×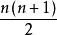
=![]() +
+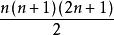 +n(n+1)
+n(n+1)
又![]() =1×(1+1)×(1+2)+2×(2+1)×(2+2)+…+n(n+1)(n+2)
=1×(1+1)×(1+2)+2×(2+1)×(2+2)+…+n(n+1)(n+2)
=![]() +
+![]() +
+![]() +…+
+…+![]()
=![]() (
(![]() +
+![]() +
+![]() +…+
+…+![]() )
)
=![]() (
(![]() +
+![]() +
+![]() +…+
+…+![]() )
)
=![]() (
(![]() +
+![]() +
+![]() +…+
+…+![]() )
)
=![]() (
(![]() +
+![]() +…+
+…+![]() )
)
=…
=![]()
![]()
=6![]()
∴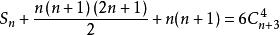
由此得![]() =
=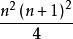 。
。
因式分解证明
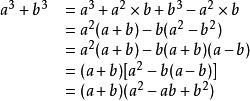
几何验证
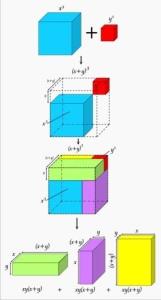 图象化立方和公式透过绘立体的图像,也可验证立方和。根据右图,设两个立方,总和为[3]:
图象化立方和公式透过绘立体的图像,也可验证立方和。根据右图,设两个立方,总和为[3]:
![]()
把两个立方体对角贴在一起,根据虚线,可间接得到:
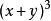
要得到![]() ,可使用
,可使用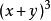 的空白位置。该空白位置可分割为3个部分:
的空白位置。该空白位置可分割为3个部分:
·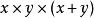
·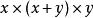
·
把三个部分加在一起,便得:
=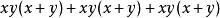
=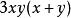
之后,把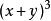 减去它,便得:
减去它,便得: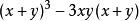 公式发现两个数项皆有一个公因子,把它抽出,并得:
公式发现两个数项皆有一个公因子,把它抽出,并得:
=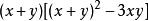
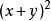 可通过完全平方公式,得到:
可通过完全平方公式,得到:
=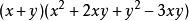
=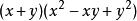
这样便可证明: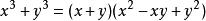

-
油耗怎么计算(油耗怎么计算公式多少钱一公里)
2025-11-02 02:18:38 查看详情 -
百公里油耗多少钱(百公里油耗多少钱怎么算公式)
2025-11-02 02:18:38 查看详情 -
怎么算油费(怎么算油费公式)
2025-11-02 02:18:38 查看详情 -
汽车油耗怎样计算(汽车油耗怎样计算公式)
2025-11-02 02:18:38 查看详情 -
发动机功率计算公式 发动机功率的计算公式及单位换算
2025-11-02 02:18:38 查看详情


 求购
求购






