- 二项展开式

二项展开式
二项式定理

其中, ,又有
,又有![]() 等记法,称为二项式系数,此系数亦可表示为杨辉三角形。等式的右边
等记法,称为二项式系数,此系数亦可表示为杨辉三角形。等式的右边 即为
即为![]() 的展开式,称为二项展开式。
的展开式,称为二项展开式。
理解
将![]() 看成
看成![]() 个
个![]() 相乘,从每个括号中取一项 (非
相乘,从每个括号中取一项 (非![]() 即
即![]() ) 相乘的所有单项式合并同类项得到的,按取
) 相乘的所有单项式合并同类项得到的,按取![]() 的个数分为
的个数分为![]() 类 ,不取
类 ,不取![]() 的是
的是![]() ,取 1 个
,取 1 个![]() 的是
的是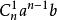 ,..., 取
,..., 取![]() 个
个![]() 的是
的是 ,...,取
,...,取![]() 个
个![]() 的是
的是![]()
注意:[1]
(1)选取性,二项式的两项怎样选取 (各取几个) 才能构成所求的项;
(2)有序性,![]() 的展 开式第
的展 开式第![]() 项是取
项是取![]() 个
个![]() (同时取
(同时取![]() 个
个![]() ), 这里的
), 这里的![]() 和
和![]() 不能互换
不能互换
(3)项 、项的系数与二项式系数的区别
某项要把这一项全部写出来;某项的系数只写这一项的系数,不带字母 (即把每个字母当作数 1) ;某项的二项式系数就是相应的组合数![]()
性质
(1)项数:n+1项
(2)第k+1项的二项式系数是![]()
(3)在二项展开式中,与首末两端等距离的两项的二项式系数相等。
(4)如果二项式的幂指数是偶数,中间的一项的二项式系数最大。如果二项式的幂指数是奇数,中间两项的的二项式系数最大,并且相等。
(5)二项式通项: ,是第
,是第![]() 项
项
证明
这里,采用数学归纳法对二项式定理进行证明
当![]() ,
,
假设二项展开式在![]() 时成立,设
时成立,设 ,则:
,则:



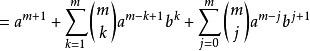 (取出
(取出![]() 的项)
的项)
 (设
(设 )
)
 ( 取出
( 取出 项)
项)
 (两者相加)
(两者相加)
 (套用帕斯卡法则)
(套用帕斯卡法则)

等式也成立
结论:对于任意自然数n,等式均成立。
例题
某项的系数
求二项展开式的某项或某项的系数是高考数学的一个基本知识点,每年的高考题都有一定的题出现。[1]
例1. 求 的展开式中
的展开式中![]() 的系数
的系数
解:![]() 要取2个,故
要取2个,故![]() 的系数是
的系数是
例2. 求 的展开式中
的展开式中![]() 的系数
的系数
解:![]() 要取4个,故
要取4个,故![]() 的系数是
的系数是
系数最值项
例. 求 展开式中系数最大项和最小项[2]
展开式中系数最大项和最小项[2]
解:
通项=
通项的系数=
设系数![]() 最大,则
最大,则
解得: ,因为
,因为![]() ,所以
,所以![]() ,故系数最大项为
,故系数最大项为![]() 和
和![]()
由于最大项在中间取得,所以最小项在两端,计算得: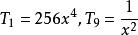 ,故系数最小项为
,故系数最小项为![]()
指定项
求二项展开式中的指定项,一般是利用通项公式进行。[3]
例. 展开式中的常数项
展开式中的常数项
解:展开式的通项= ,令
,令 ,解得
,解得![]()
故常数项为:

-
吉利/腾讯等四方展开合作 吉利新款缤越假想图曝光
2025-09-19 00:18:33 查看详情 -
吉利缤瑞COOL正式上市 吉利/腾讯等四方展开合作
2025-09-19 00:18:33 查看详情 -
吉利PREFACE内饰官图曝光 吉利/腾讯等四方展开合作
2025-09-19 00:18:33 查看详情 -
吉利/腾讯等四方展开合作 极氪为Waymo
2025-09-19 00:18:33 查看详情 -
吉利/腾讯等四方展开合作 采用全新配色
2025-09-19 00:18:33 查看详情 -
吉利/腾讯等四方展开合作 吉利星越L或将于三季度上市
2025-09-19 00:18:33 查看详情 -
吉利豪越新增车型上市 在技术支持和工程服务领域展开合作
2025-09-19 00:18:33 查看详情 -
吉利汽车回复上交所27问 在技术支持和工程服务领域展开合作
2025-09-19 00:18:33 查看详情 -
吉利星越L 吉利/腾讯等四方展开合作
2025-09-19 00:18:33 查看详情 -
试驾吉利星越L 吉利/腾讯等四方展开合作
2025-09-19 00:18:33 查看详情


 求购
求购

