- 共轭双曲线

共轭双曲线
定义
如果一条双曲线的实轴和虚轴分别是另一条双曲线的虚轴和实轴(都指线段),则两条双曲线叫作共轭的。当两条双曲线共轭时,每条双曲线都叫作另一条双曲线的共轭双曲线(图1)。[2]
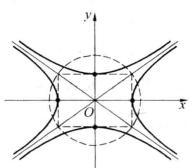 图1
图1
相关性质定理
定理双曲线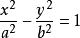 和
和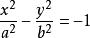 是共轭的(这两个方程等号的左端完全一样,右端的常数项一个是1,一个是一1),也就是实轴与虚轴互换的双曲线。
是共轭的(这两个方程等号的左端完全一样,右端的常数项一个是1,一个是一1),也就是实轴与虚轴互换的双曲线。
推论双曲线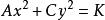 和
和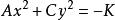 (这里A,C异号,
(这里A,C异号,![]() )共轭。
)共轭。
共轭双曲线除具有定义中所说的关系以外,还有以下的简单关系:
(1)两条共轭双曲线的四个焦点与它们的共同中心等距离,即互为共轭的双曲线的4个焦点在同一圆上,这个圆叫做双曲线的辅助圆。[3]
(2)两条共轭双曲线有共同的渐近线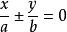 ,相同的焦距,但焦点不一样。
,相同的焦距,但焦点不一样。
(3)互为共轭的双曲线的两个离心率的倒数平方和为1。[4]
这是因为两条共轭双曲线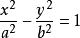 和
和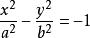 的渐近线都是
的渐近线都是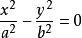 ,即都是
,即都是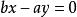 和
和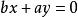 。
。
考察方程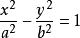 ,
,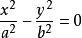 ,
,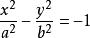 。
。
前后两个是共轭双曲线的方程,中间是它们的共同渐近线的方程,这三个方程的等号左端完全一样,而等号右端的常数项恰成等差数列。[2]
例题解析
例1已知双曲线的中心在原点,焦点在一条坐标轴上,它的一条渐近线为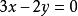 ,并且双曲线通过点
,并且双曲线通过点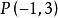 ,求这双曲线的方程。[2]
,求这双曲线的方程。[2]
解:因双曲线的中心在原点,并且焦点在一条坐标轴上,所以双曲线的两条渐近线关于坐标轴对称,因此另一条渐近线为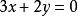 ,所以两条渐近线的方程为
,所以两条渐近线的方程为
![]() 即
即
![]() 因此双曲线的方程应该是
因此双曲线的方程应该是
![]() 由于这条双曲线通过点
由于这条双曲线通过点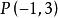 ,所以有
,所以有
![]() 从而
从而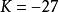 ,所以双曲线的方程为
,所以双曲线的方程为
![]()
例2设一条直线和一条双曲线及其两条渐近线都相交,求证:这条直线夹在双曲线及其渐近线之间的两条线段(图2中的AB与CD)相等。[2]
证明:设双曲线的方程为
![]() 那么,它的渐近线的方程为
那么,它的渐近线的方程为
![]() 设割线的方程为
设割线的方程为
![]() 则方程组
则方程组
![]() 的解是交点B,C的坐标.把
的解是交点B,C的坐标.把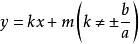 代入
代入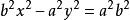 ,得
,得
![]() 这个二次方程的两个根
这个二次方程的两个根![]() 和
和![]() 分别为B和C的横坐标,而
分别为B和C的横坐标,而
![]() 于是线段BC的中点的横坐标
于是线段BC的中点的横坐标
![]() 线段BC的中点的纵坐标
线段BC的中点的纵坐标
![]() 要求A,D的坐标,应解方程组
要求A,D的坐标,应解方程组
![]() 很明显,消去
很明显,消去![]() 后所得的二次方程的二次项和一次项与
后所得的二次方程的二次项和一次项与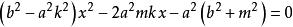 相同,因此它的两个根的和,即A,D的横坐标的和与B,C的横坐标的和相等,从而线段AD的中点的横坐标与线段BC的中点的横坐标相等,因而线段AD的中点的纵坐标与线段BC的中点的纵坐标也相等。这样,线段AD的中点与线段BC的中点实际上是同一个点,所以线段AB等于线段CD。
相同,因此它的两个根的和,即A,D的横坐标的和与B,C的横坐标的和相等,从而线段AD的中点的横坐标与线段BC的中点的横坐标相等,因而线段AD的中点的纵坐标与线段BC的中点的纵坐标也相等。这样,线段AD的中点与线段BC的中点实际上是同一个点,所以线段AB等于线段CD。
当割线与双曲线的实对称轴垂直时,由双曲线及其渐近线的对称性可知也有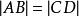 。
。
说明;若移动割线,变为双曲线的切线时,由本例可知,这切线夹在两渐近线间的线段被切点二等分(图3)。[2]
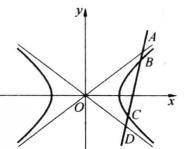 图2
图2
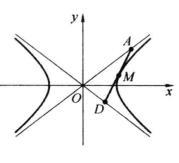 图3
图3



 求购
求购








