- 莱布尼茨公式

莱布尼茨公式
基础信息
不同于牛顿-莱布尼茨公式,莱布尼茨公式用于对两个函数的乘积求取其高阶导数,[2]
一般的,如果函数u=u(x)与函数v=v(x)在点x处都具有n阶导数,那么此时有
(uv)(n)= u(n)v+ nu(n-1)v' +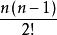 u(n-2)v" +
u(n-2)v" +![]() +
+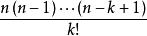 u(n-k)v(k)+
u(n-k)v(k)+![]() + uv(n)
+ uv(n)
也可记为
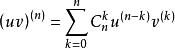
推导过程
如果存在函数u=u(x)与v=v(x),且它们在点x处都具有n阶导数,那么显而易见的,
u(x) ± v(x) 在x处也具有n阶导数,且 (u±v)(n)= u(n)± v(n)
至于u(x) × v(x) 的n阶导数则较为复杂,按照基本求导法则和公式,可以得到:
(uv)' = u'v + uv'
(uv)'' = u''v + 2u'v' + uv''
(uv)''' = u'''v + 3u''v' + 3u'v'' + uv'''
…………
运用数学归纳法可证[3]
(uv)(n)= u(n)v + nu(n-1)v' +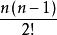 u(n-2)v" +
u(n-2)v" +![]() +
+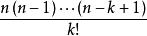 u(n-k)v(k)+
u(n-k)v(k)+![]() + uv(n)
+ uv(n)
上式便称为莱布尼茨公式(Leibniz公式)
区别
由于名称相似,不少人将牛顿-莱布尼茨公式与莱布尼茨公式相混淆,事实上他们是两个完全不同的公式。
牛顿-莱布尼茨公式是微积分学中的一个重要公式,它把不定积分与定积分相联系了起来,也让定积分的运算有了一个完善、令人满意的方法。其基本形式为
![]()
而莱布尼茨公式是导数计算中会使用到的一个公式,它是为了求取两函数乘积的高阶导数而产生的一个公式。
二者存在本质上的区别。
相关人物
戈特弗里德·威廉·莱布尼茨
弗里德·威廉·莱布尼茨(Gottfried Wilhelm Leibniz,1646年—1716年),德国哲学家、数学家,和牛顿先后独立发明了微积分。有人认为,莱布尼茨最大的贡献不是发明微积分,而是微积分中使用的数学符号,因为牛顿使用的符号普遍认为比莱布尼茨的差。他所涉及的领域及法学、力学、光学、语言学等40多个范畴,被誉为十七世纪的亚里士多德。
 戈特弗里德·威廉·莱布尼茨
戈特弗里德·威廉·莱布尼茨

-
油耗怎么计算(油耗怎么计算公式多少钱一公里)
2025-09-29 08:03:13 查看详情 -
百公里油耗多少钱(百公里油耗多少钱怎么算公式)
2025-09-29 08:03:13 查看详情 -
怎么算油费(怎么算油费公式)
2025-09-29 08:03:13 查看详情 -
汽车油耗怎样计算(汽车油耗怎样计算公式)
2025-09-29 08:03:13 查看详情 -
发动机功率计算公式 发动机功率的计算公式及单位换算
2025-09-29 08:03:13 查看详情


 求购
求购





