- 振动跃迁

振动跃迁
纯振动跃迁
 图1作为一级近似,可用谐振子模型描述双原子分子的振动。一个简单的谐振子是一个力学体系,它由点质量m和无质量弹簧所组成。作用在此质量上的恢复力与质点从其平衡位置的位移及弹簧的力常数k成正比。势能V与此位移的平方成正比,振动频率v则由式
图1作为一级近似,可用谐振子模型描述双原子分子的振动。一个简单的谐振子是一个力学体系,它由点质量m和无质量弹簧所组成。作用在此质量上的恢复力与质点从其平衡位置的位移及弹簧的力常数k成正比。势能V与此位移的平方成正比,振动频率v则由式 给出。
给出。
同样,对于双原子分子,V是原子核间距r从其平衡位置![]() 的位移q(或折合质量为
的位移q(或折合质量为![]() 真的粒子从重心的位移)的函数。此势能函数呈抛物线形,如方程12-4所示(此处讨论的所有方程见图1)。在Schrodinger方程中,用这一势能函数得到的结果是方程(12-5)所描述的量子化能级。在光谱的中或远红外区可观察到振动吸收跃迁。
真的粒子从重心的位移)的函数。此势能函数呈抛物线形,如方程12-4所示(此处讨论的所有方程见图1)。在Schrodinger方程中,用这一势能函数得到的结果是方程(12-5)所描述的量子化能级。在光谱的中或远红外区可观察到振动吸收跃迁。
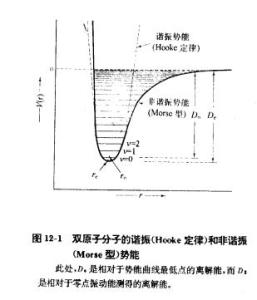 图2仅在接近平衡核间距时,实际的振动势能才能非常好地符合抛物线函数。对于所有的间距,表示在方程(12-8)中的Morse势能函数才能更接近地符合分子振动的势能。这一函数的形状及所观察到的双原子分子的振动能级显示在图2中。若在Schrodinger方程中用Morse势能函数,则解会更复杂。方程(12-9)是由非谐振子模型得到的能级近似解,方程(12-9)中第二项导致在接近分子解离限的大小v值处可观察到能级的收敛性。谐振子模型预期所有能级都按
图2仅在接近平衡核间距时,实际的振动势能才能非常好地符合抛物线函数。对于所有的间距,表示在方程(12-8)中的Morse势能函数才能更接近地符合分子振动的势能。这一函数的形状及所观察到的双原子分子的振动能级显示在图2中。若在Schrodinger方程中用Morse势能函数,则解会更复杂。方程(12-9)是由非谐振子模型得到的能级近似解,方程(12-9)中第二项导致在接近分子解离限的大小v值处可观察到能级的收敛性。谐振子模型预期所有能级都按![]() 等距离分布,且允许键断裂。
等距离分布,且允许键断裂。
振动能级间跃迁选律为![]() ,此外,必须发生偶极矩变化,以致在1R吸收光谱中同核双原子分子并不显示振动跃迁。有时可观察到叫做泛频的弱跃迁,这些跃迁对应于
,此外,必须发生偶极矩变化,以致在1R吸收光谱中同核双原子分子并不显示振动跃迁。有时可观察到叫做泛频的弱跃迁,这些跃迁对应于![]() =2或3。
=2或3。
振动能级的通常能量间隔大约为![]() 。由Boltzmann分布可以看出,不存在外部辐射时,在室温下处于激发态的分子通常为1%或更少。因此在室温下,观察到最多的吸收跃迁是从v=0能级到v=1能级。
。由Boltzmann分布可以看出,不存在外部辐射时,在室温下处于激发态的分子通常为1%或更少。因此在室温下,观察到最多的吸收跃迁是从v=0能级到v=1能级。
CO2的振动跃迁
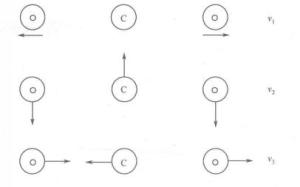 图3
图3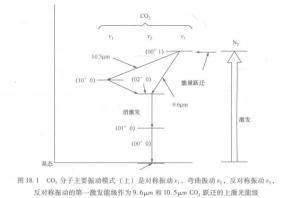 图4图3表示CO2分子的三种主要振动模式:对称振动模式
图4图3表示CO2分子的三种主要振动模式:对称振动模式![]() ;弯曲模式口
;弯曲模式口![]() ;反对称振动模式
;反对称振动模式![]() 。如图4所示,每种振动模式有其本身的量子化能级分布。这些模式中,弯曲模式的能级最小,对称振动模式能级约为弯曲模式的两倍,反对称振动模式的能级则更大。
。如图4所示,每种振动模式有其本身的量子化能级分布。这些模式中,弯曲模式的能级最小,对称振动模式能级约为弯曲模式的两倍,反对称振动模式的能级则更大。
这些振动能级中成对能级问的跃迁形成振动激光器。和四能级电子跃迁激光器一样,外部能量源使反转粒子增加到泵浦能级。分子迅速从泵浦能级衰退到长寿命亚稳态,处于上激光能级,然后激发辐刺使分子降低至下激光能级,最后衰退至基态。所有的四个能级都是基态电子能级中的振动能级。
振动跃迁对应于1~100μm的红外波长,因此比电子跃迁需要较少的激励能量。但需要注意的是每个振动能级伴随数十种转动能级。量子力学的法则要求当分子从一个振动能级运动到另一振动能级时,需要精确的改变一个转动能级。想一想这个要求的含义,如果分子开始于上振动能级的第三转动能级,其必须终止于下振动能级的第二或第四转动能级;如果其开始于第六转动能级,其必须终止于第五或第七转动能级,结果是每个振动跃迁包含可能的转动跃迁。所有的努力使振动激光器发射出一个较宽范围的波长,对应振动跃迁加上(或减去)转动跃迁的能量。
CO2激光是上述工作模式的典型代表。如图4所示,首先被激励的CO2的反对称振动是两激光跃迁的上激光能级。如果受激发的分子衰退至对称振动的第一激发态,其释放一个名义波长10.5μm的光子。或者,它衰退至转动模式的第二激发能级,释放9.6μm的光子。10.5μm的跃迁较强,但是激光器可以同时在两个波长上振荡。
 图5如图5所示,每种振动跃迁有其自身的一族转动跃迁。距离振动跃迁名义中心的每个间隔对应转动能量的一个能级间隔。CO2激光可以同时在一条或者多条谱线上振荡取决于谐振腔镜。为能量传输设计的工业用激光器运行在较宽带宽上,其名义波长为10.6μm,但实际出射光线在9~11μm之间。科学研究用激光器和某些有特殊用途的激光器通常将振荡限制在带宽的一小部分或者一个单一的转动谱线上。
图5如图5所示,每种振动跃迁有其自身的一族转动跃迁。距离振动跃迁名义中心的每个间隔对应转动能量的一个能级间隔。CO2激光可以同时在一条或者多条谱线上振荡取决于谐振腔镜。为能量传输设计的工业用激光器运行在较宽带宽上,其名义波长为10.6μm,但实际出射光线在9~11μm之间。科学研究用激光器和某些有特殊用途的激光器通常将振荡限制在带宽的一小部分或者一个单一的转动谱线上。
转动-振动跃迁
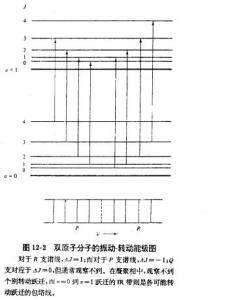 图6在高分辨率情况下观察气态双原子分子的振动光谱时可发现,每一个谱带都含有大量距离靠得很近的组分。由于这一点,分子光谱常叫做带光谱。根据振动跃迁期间转动的激发可解释观察到的结构,这种振动转动光谱的形状可由振动一转动分子的能级预测。对简单的双原子分子且不用非谐性和离心校正的情况下,方程(12一10,见图1)给出了以波数为单位时可能发生的跃迁的能量。
图6在高分辨率情况下观察气态双原子分子的振动光谱时可发现,每一个谱带都含有大量距离靠得很近的组分。由于这一点,分子光谱常叫做带光谱。根据振动跃迁期间转动的激发可解释观察到的结构,这种振动转动光谱的形状可由振动一转动分子的能级预测。对简单的双原子分子且不用非谐性和离心校正的情况下,方程(12一10,见图1)给出了以波数为单位时可能发生的跃迁的能量。
由v到v+1的振动吸收跃迁可产生三组称作支的谱线,如图6所示。较低频率的P支对应于△v=1和△J=-1的跃迁,而Q支对应于△v=1和△J=0的跃迁。而较高频率的Q支对应△v=1和△J=+1的跃迁,除了具有奇数个电子的双原子分子(例如NO)除外,对双原子分子观察不到Q支。在吸收光谱中,R和P带中各组分的相对强度则由振动基态中各转动能级的布居和简并度所决定。

-
汽车振动噪声控制技术
2025-08-07 00:06:28 查看详情 -
汽轮发电机组的振动及现场平衡
2025-08-07 00:06:28 查看详情 -
ZH6938型低频振动传感器
2025-08-07 00:06:28 查看详情


 求购
求购




