叶子结点

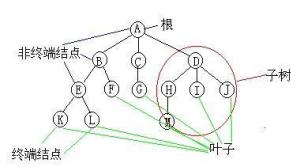叶子结点叶子结点 就是出度为0的结点 就是没有子结点的结点

n₀：出度为0的结点数，n₁:度为1的结点 n₂：度为2的结点数。 N是总结点

在二叉树中：

n₀=n₂+1；

N=n₀+n₁+n₂

一棵树度为4，其中度为1，2，3，4的结点个数分别为4，2，1，1，则这棵树的叶子节点个数为多少？

解：因为任一棵树中，结点总数=度数*该度数对应的结点数+1，所以：

总结点数=1*4+2*2+3*1+4*1+1=16

叶子结点数=16-4-2-1-1（总节点数－度不为0的个数）=8

则：n0=8

其中：n0表示叶子结点。

该算法的递归形式比较容易实现。

具体的代码块如下：

int leaf(BiTree root)

{

static int leaf_count = 0; --->在递归调用时只进行一次初始化。

if (NULL != root) {

leaf(root->lchild);

leaf(root->rchild);

if (root->lchild == NULL

&& root->rchild == NULL)

leaf_count++;

}

return leaf_count;

}

1，该算法的代码模块的独立性算是设计的比较好的。

1.1，耦合比较低，传入树的树根，返回树的叶子节点的个数。

1.2，内聚比较高，模块中的代码比较紧密。容易阅读，易维护。

2，该算法是用递归实现的，效率肯定不是很高。

3，该算法是在对树的后序遍历的基础上实现的。如果该节点的左子树，再右子树，

最后是根节点。