线性函数

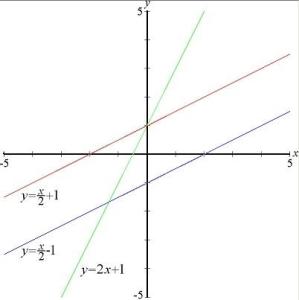红、蓝直线斜率相同，红、绿直线 y截距相同在初级代数与解析几何，线性函数是只拥有一个变量的一阶多项式函数，又或者是常数函数。因为，采用直角坐标系，这些函数的图象是直线，所以，这些函数是线性的。要注意的是，与x轴垂直的直线不是线性函数。（因为输入值不对应唯一输出值，所以它不符合函数的定义）

线性函数可以表达为斜截式：

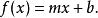
其中m是斜率且，而是在y轴上的截距，即函数图象与 y轴相交点的-坐标。改变斜率会使直线更陡峭或平缓。改变-截距会将直线移上或移下。

右图展示了三个线性函数的图象：

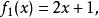
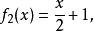
红色与蓝色直线的斜率相同。 红色与绿色直线的-截距相同。

线性变换：

在线性代数里，线性函数是一个线性映射。

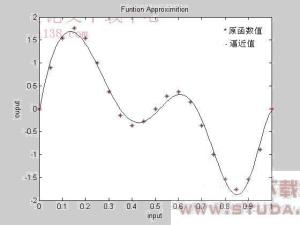
设V和W是在相同域K上的向量空间。函数f:V→W被称为是线性映射，如果对于V中任何两个向量a和b与K中任何标量k，满足下列两个条件：

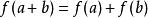
非线性函数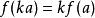

即其维持向量加法与标量乘法。

如果W等同域K，也称f是V上的一个线性函数。

例如，假若，我们用坐标向量(Coordinate vector) 来表示x与f(x)，那么线性函数可以表达为

f(x)=M*x；其中，M是矩阵。

两个变量之间存在一次函数关系，就称它们之间存在线性关系。

正比例关系是线性关系中的特例，反比例关系不是线性关系。

更通俗一点讲，如果把这两个变量分别作为点的横坐标与纵坐标，其图象是平面上的一条直线，则这两个变量之间的关系就是线性关系。

在高等数学里，线性函数是一个线性映射，是在两个向量空间之间，维持向量加法与标量乘法的映射。

例如，假若，我们用坐标向量(coordinate vector来表示与。那么，线性函数可以表达为

其中，是矩阵。

仿射变换是指一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。

一个对向量平移，与旋转放大缩小的仿射映射为

上式在齐次坐标上，等价于下面的式子

在分形的研究里，收缩平移仿射映射可以制造制具有自相似性的分形。

一个在两个仿射空间之间的仿射变换，是在向量上呈现线性之坐标点的变换（即为空间中点与点之间的向量）。以符号表示的话，使得，决定任一对点的线性变换：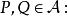

或者

仿射变换表示

如上所示，仿射变换为两函数的复合：平移及线性映射。普通向量代数用矩阵乘法呈现线性映射, 用向量加法表示平移。正式言之，于有限维度之例中，假如该线性映射被表示为一矩阵“A”，平移被表示为向量，一仿射映射可被表示为^[1]