- 非负数
非负数
定义
所谓非负数，是指零和正实数。非负数的性质在解题中颇有用处，常见的非负数有三种：实数的偶次幂、实数的绝对值和算术根。[2]
类型
实数的偶次幂是非负数
若
是任意实数，则
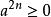(n为正整数)，特别地，当n=1时，有
。
实数的绝对值是非负数
若是实数．则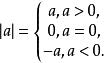
性质：绝对值最小的实数是零。
算术根及其中的被开方数
是算术根，则
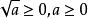。[3]
性质：一个正实数的算术根是非负数，若
是实数，则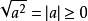
。
三个实数平方和与两两积之和的差
非负数的其他性质
①数轴上，原点和原点右边的点表示的数都是非负数。
②有限个非负数的和仍为非负数，即若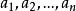
为非负数，则
。
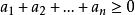③有限个非负数的和为零，那么每一个加数也必为零，即若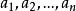为非负数，且
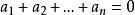，则必有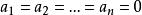
。
在利用非负数解决问题的过程中，这条性质使用得最多。
④非负数的积和商(除数不为零)仍为非负数。
⑤最小非负数为零，没有最大的非负数。
⑥一元二次方程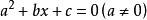
有实数根的充要条件是判别式
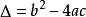为非负数。
应用非负数解决问题的关键在于能否识别并揭示出题目中的非负数，正确运用非负数向有关概念及其性质，巧妙地进行相应关系的转化，从而使问题得到解决。[2]
非负数的应用
利用非负数求代数式的值
例1已知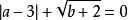
．求
的值。
讲解由题意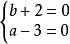
，解得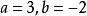
。
代入代数式得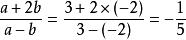
。
评注本题利用绝对值和根式的非负数性质求解，比较容易简单。[2]
利用非负数求最值
例2已知
为实数，求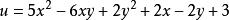
的最小值和取得最小值时的的值。
讲解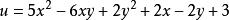
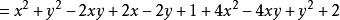
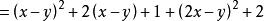
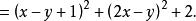
因为为实数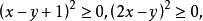，所以
，所以
。
所以当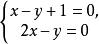
时，
有最小值2，此时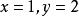
。
评注利用非负数求最值，需对问题条件进行变形，写成非负数形式是关键。[2]
利用非负数求方程的根或个数
例3确定方程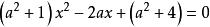
的实数根的个数。
讲解(方法一) 将原方程化为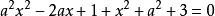
，
即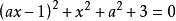
，
对于任意实数x，均有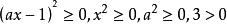
，
所以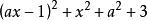
恒大于0，
故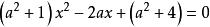无实根。
(方法二) 利用判别式判断。
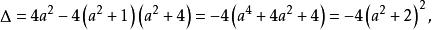
因为判别式小于零，所以无解。
评注本题确定方程根的个数，首先判断方程类型尤其重要。[2]
求购