- 凹函数

凹函数
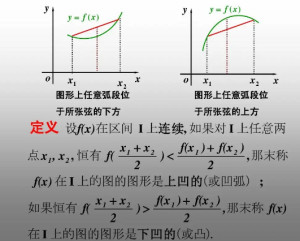
定义
如果定义在某一区间上的一元实函数是连续函数,且对这一区间中的任何两点X1、X2,当X1<X2时,有不等式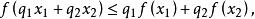 其中q1、q2为正数,q1+q2=1,这时,我们把函数f(x)叫做凹函数,或叫做下凸函数。
其中q1、q2为正数,q1+q2=1,这时,我们把函数f(x)叫做凹函数,或叫做下凸函数。
如果把上述条件中的“≥”改成“>”,则叫做严格凹函数,或叫做严格下凸函数。
如果y=f(x)是(严格)凹函数,那么它的图象是(严格)凹曲线,或叫做(严格)下凸曲线。
凹函数的概念是詹森(J.L.w.v.Jermen,1859~1925)引入的,他所采取的定义条件是
![]()
相当于上述定义中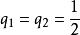 的特殊情况形。这种定义对于连续函数来说是等价的。
的特殊情况形。这种定义对于连续函数来说是等价的。
如果f(x)是凹函数,那么-f(x)即是凸函数,通常都是把凹函数转化为凸函数来研究。
如果一元实函数f(x)在某区间二阶可导,那么这一函数为凹函数的充要条件是在这一区间上恒有f‘’(x)≥0(对于严格凹函数,只要改成f‘’(x)>0就可以了)。[1]
与凸函数(下凸)对比,这里的凹函数(上凸)应有:如果其二阶导数在区间上恒大于等于0,就称为凹函数。如果其二阶导数在区间上恒小于0,就称为严格凸函数。
在数学当中,凹函数是凸函数的相反。
性质
 凹函数(3)如果一个可微函数f它的导数f'在某区间是单调上升的,也就是二阶导数若存在,则在此区间,二阶导数是大于零的,f就是凹的;即一个凹函数拥有一个下跌的斜率(当中下跌只是代表非上升而不是严谨的下跌,也代表这容许零斜率的存在。)
凹函数(3)如果一个可微函数f它的导数f'在某区间是单调上升的,也就是二阶导数若存在,则在此区间,二阶导数是大于零的,f就是凹的;即一个凹函数拥有一个下跌的斜率(当中下跌只是代表非上升而不是严谨的下跌,也代表这容许零斜率的存在。)
如果一个二次可微的函数f,它的二阶导数f'(x)是正值(或者说它有一个正值的加速度),那么它的图像是凹的;如果二阶导数f'(x)是负值,图像就会是凸的。当中如果某点转变了图像的凹凸性,这就是一个拐点。
如果凹函数(也就是向上开口的)有一个“底”,在底的任意点就是它的极小值。如果凸函数有一个“顶点”,那么那个顶点就是函数的极大值。
如果f(x)是二次可微的,那么f(x)就是凹的当且仅当f''(x)是非正值。如果二阶导数是负值的话它就是严谨凹函数,但相反而言又不一定正确。
证明
设函数f(x)在定义域内连续可导且满足f''(x)>0;设x1<x2,0<a<1、证明:f[ax1+(1-a)x2]<af(x1)+(1-a)f(x2);(即利用凹函数的充要条件来证明其定义。)
因ax1+(1-a)x2-x1=(1-a)(x2-x1)>0;
则x1<ax1+(1-a)x2;
根据拉格朗日中值定理。
必存在x1<μ< ax1+(1-a)x2;
使f[ax1+(1-a)x2]-f(x1)= (1-a)(x2-x1)f'(μ);
同理。
存在ax1+(1-a)x2<ξ<x2;
使f(x2)- f[ax1+(1-a)x2]= a(x2-x1)f'(ξ);
故a{f[ax1+(1-a)x2]-f(x1)}- (1-a){f(x2)- f[ax1+(1-a)x2]}=a (1-a)(x2-x1)[f’(μ)- f’(ξ)];
根据拉格朗日中值定理。
有μ<δ<ξ;
f'(μ)- f'(ξ)=(μ-ξ)f''(δ);
因f''(x)>0;
则f'(μ)- f'(ξ)<0;
则a{f[ax1+(1-a)x2]-f(x1)}- (1-a){f(x2)- f[ax1+(1-a)x2]}<0;
整理后得f[ax1+(1-a)x2]<af(x1)+(1-a)f(x2);
同理,若f''(x)≤0,则结果相反 。
即若f''(x)≤0,则f[ax1+(1-a)x2]≥af(x1)+(1-a)f(x2);满足凹函数的定义。
证明完毕;
注意:中国某些机构关于函数凹凸性定义和国外的定义是相反的。Convex Function在某些中国大陆的数学书中指凹函数。Concave Function指凸函数。但在中国大陆涉及经济学的很多书中,凹凸性的提法和其他国家的提法是一致的,也就是和数学教材是反的。举个例子,同济大学高等数学教材对函数的凹凸性定义与本条目相反,本条目的凹凸性是指其上方图是凹集或凸集,而同济大学高等数学教材则是指其下方图是凹集或凸集,两者定义正好相反。
应用举例
线性函数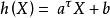 是E[2]
是E[2]

-
1641函数信号发生器
2025-09-21 21:58:28 查看详情


 求购
求购









