成像公式

凸透镜的成像规律是 1/u+1/v=1/f（即： 物距的倒数与 像距的倒数之和等于焦距的倒数。）一共有两种推导方法 。分别为“几何法”与“函数法”

【题】如右图 ，用几何法证明1/u+1/v=1/f。

【解】∵△ABO∽△A'B'O

∴AB:A'B'=u:v

∵△COF∽△A'B'F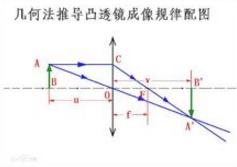

∴CO:A'B'=f:(v-f)

∵四边形ABOC为矩形

∴AB=CO

∴AB:A'B'=f:(v-f)

∴u:v=f:(v-f)

∴u(v-f)=vf

∴uv-uf=vf

∵uvf≠0

∴(uv/uvf)-(uf/uvf)=vf/uvf

∴1/f-1/v=1/u

即： 1/u+1/v=1/f

【题】 如右图 ，用函数法证明1/u+1/v=1/f。

【解】 一基础

右图为 凸透镜成像示意图。

其中c为成像的物体长度，d为物体成的像的长度。u为 物距，v为 像距，f为焦距。

步骤

（一）为便于用函数法解决此问题，将 凸透镜的 主光轴与 平面直角坐标系的横 坐标轴（x轴）关联（即重合），将凸透镜的理想折射面与纵坐标轴（y轴）关联，将凸透镜的 光心与坐标原点关联。则：点A的坐标为（-u,c），点F的坐标为（f,0），点A'的坐标为（v,-d），点C的坐标为（0，c）。

（二）将AA’，A'C双向延长为直线l1,l2，视作两条函数图象。由图象可知：直线l1为 正比例函数图象，直线l2为 一次函数图象。

（三）设直线l1的解析式为y=k1x,直线l2的解析式为y=k2x+b

依题意，将A(-u,c),A'(v,-d),C(0,c)代入相应解析式得方程组：

c=-u·k1

-d=k2v+b

c=b

把k1,k2当成未知数解之得：

k1=-(c/u)k2=-(c/f)

∴两 函数解析式为：

y=-(c/u)x y=-(c/f)x+c

∴两函数交点A'的坐标（x,y)符合方程组

y=-(c/u)x

y=-(c/f)x+c

∵A'(v,-d)

∴代入得：

-d=-(c/u)v

-d=-(c/f)v+c

∴-(c/u)v=-(c/f)v+c=-d

∴(c/u)v=(c/f)v-c=d

cv/u=(cv/f)-c

fcv=ucv-ucf

fv=uv-uf

∵uvf≠0

∴fv/uvf=(uv/uvf)-(uf/uvf)

∴1/u=1/f-1/v

即： 1/u+1/v=1/f

人类的眼睛所成的像，是 实像还是 虚像呢？我们知道， 人眼的结构相当于一个凸透镜，那么外界物体在视网膜上所呈的像，一定是实像。根据上面的经验规律，视网膜上的物像似乎是倒立的。可是我们平常看见的任何物体，明明是正立的啊？这个与经验与规律发生冲突的问题，实际上涉及到 大脑皮层的调整作用以及生活经验的影响。由于 视觉错误，人眼认为光是由物体发出并直射入人眼。

当物体与凸 透镜的距离大于透镜的焦距时，物体成倒立的像，当物体从较远处向透镜靠近时，像逐渐变大，像到透镜的距离也逐渐变大；当物体与透镜的距离小于焦距时，物体成放大的像，这个像不是实际 折射光线的会聚点，而是它们的 反向延长线的交点，用光屏接收不到，是虚像。平面镜所成的虚像对比（不能用光屏接收到，只能用眼睛看到）。

照相机的镜头就是一个 凸透镜，要照的景物就是物体，胶片就是屏幕。照射在物体上的光经过 漫反射通过凸透镜将物体的像成在最后的胶片上；胶片上涂有一层对光敏感的物质，它在 曝光后发生 化学变化，物体的像就被记录在 胶卷上

而 物距、 像距的关系与 凸透镜的成像规律完全一样。物体靠近时，像越来越远，越来越大，最后再同侧成虚像。物距增大，像距减小，像变小；物距减小，像距增大，像变大。一倍焦距分虚实， 二倍焦距分大小。

放映机, 幻灯机，投影机，放大镜, 探照灯,摄像机和摄像头都应用了 凸透镜，凸透镜完善了我们的生活，时时刻刻都应用在生活中。远视眼镜就是凸透镜， 近视眼镜就是 凹透镜。

另外凸透镜还用于：

1、拍摄、录像

2、投影，幻灯，电影

3、用于特效灯光（聚焦成各种花色）

4、成虚像用于放大文字、工件、地图等