- 复相关系数

复相关系数
基本内容
复相关系数是度量复相关程度的指标,它可利用单相关系数和偏相关系数求得。
复相关系数越大,表明要素或变量之间的线性相关程度越密切。多重相关的实质就是Y的实际观察值与由p个自变量预测的值的相关[1]。
计算方法
复相关系数是测量一个变量与其他多个变量之间线性相关程度的指标。它不能直接测算,只能采取一定的方法进行间接测算。
测定一个变量y与其他多个变量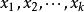 之间的相关系数。
之间的相关系数。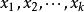 不能直接测算。可以考虑构造一个关于
不能直接测算。可以考虑构造一个关于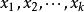 的线性组合,通过计算该线性组合与y之间的简单相关系数作为变量y与
的线性组合,通过计算该线性组合与y之间的简单相关系数作为变量y与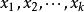 之间的复相关系数。
之间的复相关系数。
具体过程如下:
第一步,用y对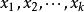 作回归,得:
作回归,得: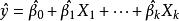 。
。
第二步,计算简单相关系数,即为y与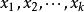 之间的复相关系数。
之间的复相关系数。
复相关系数的计算公式为: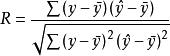 ,Matlab里面的函数 R=corrcoef(X,Y)[1]。
,Matlab里面的函数 R=corrcoef(X,Y)[1]。
比较
简单相关系数:计学家卡尔·皮尔逊设计的统计指标,或称线性相关系数、皮氏积矩相关系数等,是衡量两个随机变量之间线性相关程度的指标,通常以r表示。公式为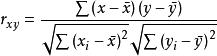 。
。
复相关系数:反映一个因变量与一组自变量(两个或两个以上)之间相关程度的指标,是度量复相关程度的指标。通常以R表示。计算公式为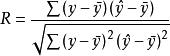 。
。
复相关系数与简单相关系数的区别是简单相关系数的取值范围是[-1,1],而复相关系数的取值范围是[0,1]。这是因为,在两个变量的情况下,回归系数有正负之分,所以在研究相关时,也有正相关和负相关之分;但在多个变量时,偏回归系数有两个或两个以上,其符号有正有负,不能按正负来区别,所以复相关系数也就只取正值[1]。
实际应用
为了解决多个因变量Y和多个自变量X之间的相关分析,假设X与Y的联合正态分布已知,而且X与Y存在线性相依,提出广义复相关系数的定义、估计和检验。广义复相关系数是简单相关系数和复相关系数的自然推广,应用上更为方便。
例如,在定量评价公路运输的技术效率和规模效率时,可以采用复相关系数对投入指标进行处理,更准确反应公路系统的投入情况,将交通事故率纳入产出指标,综合考虑了公路经济效益和外部性。[2]在研究晶体管噪声模型复相关系数与其内部噪声源的关系时,通过给出了晶体管噪声功率谱复相关系数的定义及其计算公式,对复相关系数的实部和虚部在不同频段进行了理论分析。通过复相关系数的实测结果与理论分析相符合,从而可以根据晶体管内部噪声源的情况,对复相关系数γ的大小作出估计。[3]

-
大众TALAGON/皇冠陆放领衔 与三家公司建立合作关系
2025-09-28 02:33:37 查看详情 -
长城与SQ集团汇鸿汽车达成合作伙伴关系 将于上海车展首发亮相
2025-09-28 02:33:37 查看详情 -
长安UNI 风阻系数0.27Cd
2025-09-28 02:33:37 查看详情 -
大众途锐级别全新电动车正在研发 与三家公司建立合作关系
2025-09-28 02:33:37 查看详情 -
长城与SQ集团汇鸿汽车达成合作伙伴关系 诠释独特设计美学
2025-09-28 02:33:37 查看详情 -
大众ID.4原型车实车曝光 与三家公司建立合作关系
2025-09-28 02:33:37 查看详情 -
全新大众Passat旅行版最新谍照 与三家公司建立合作关系
2025-09-28 02:33:37 查看详情


 求购
求购



