- 异或

异或
运算法则
 异或(3)1. a ⊕ a = 0
异或(3)1. a ⊕ a = 0
2. a ⊕ b = b ⊕ a
3. a ⊕b ⊕ c = a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c;
4. d = a ⊕ b ⊕ c 可以推出 a = d ⊕ b ⊕ c.
5. a ⊕ b ⊕ a = b.
6.若x是二进制数0101,y是二进制数1011;
则x⊕y=1110
只有在两个比较的位不同时其结果是1,否则结果为0
即“两个输入相同时为0,不同则为1”!
| 输入 | 运算符 | 输入 | 结果 |
| 1 | ⊕ | 0 | 1 |
| 1 | ⊕ | 1 | 0 |
| 0 | ⊕ | 0 | 0 |
| 0 | ⊕ | 1 | 1 |
逻辑
| 输入 | 运算符 | 输入 | 结果 |
| 1 | ⊕ | 0 | 1 |
| 1 | ⊕ | 1 | 0 |
| 0 | ⊕ | 0 | 0 |
| 0 | ⊕ | 1 | 1 |
作用
逻辑表达式:F=AB’⊕A’B((AB’⊕A’B)’=AB⊙A’B’,⊙为“同或”运算)
异或逻辑的真值表如图1所
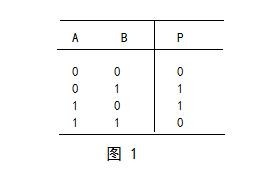 示,其逻辑符号如图2所示。异或逻辑的关系是:当AB不同时,输出P=1;当AB相同时,输出P=0。“⊕”是异或运算符号,异或逻辑也是与或非逻辑的组合,其逻辑表达式为:
示,其逻辑符号如图2所示。异或逻辑的关系是:当AB不同时,输出P=1;当AB相同时,输出P=0。“⊕”是异或运算符号,异或逻辑也是与或非逻辑的组合,其逻辑表达式为:
P=A⊕B
由图1可知,异或运算的规则是
0⊕0=0,0⊕1=1
1⊕0=1,1⊕1=0
口诀1:相同取0,相异取1
口诀2:
输入A取0,则输出p=输入B
输入A取1,则输出p=输入B的反

事实上,XOR 在英文里面的定义为either one (is one), but not both, 也即只有一个为真(1)时,取真(1)。
巧用
在计算机中普遍运用,异或(xor)的逻辑符号一般用xor,也有用⊕的:
真⊕假=真
假⊕真=真
假⊕假=假
真⊕真=假
或者为:
True ⊕ False = True
False ⊕ True = True
False ⊕ False = False
True ⊕ True = False
部分计算机语言用1表示真,用0表示假,所以两个字节按位异或如下
| 00000000 | |
| xor | 00000000 |
| ------------- | |
| 结果 | 00000000 |
下面是两个二进制数值进行异或计算:
| 11111111 | |
| xor | 00000000 |
| -------------- | |
| 结果 | 11111111 |
现实中用的都是十进制的数值,那么我们来看一看两个十进制数值是怎么进行异或计算:
5 ⊕ 3 = ?
1.进行异或计算前会把数值都转换为二进制:
5和3转为二进制分别为:0101 、0011
| 0101 | |
| xor | 0011 |
| -------- | |
| 结果 | 0110 |
2.再把结果 0110 转换为十进制的:6
3.所以 5 ⊕ 3 = 6
词条图册
| 00000000 | |
| xor | 00000000 |
| ------------- | |
| 结果 | 00000000 |



 求购
求购

