测地线方程

抽象指标下某时空的测地线方程形式为^[1]：

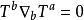其中，

分别是测地线的切矢量和该时空的协变导数。

若考虑某一坐标系{xμ}，测地线方程可以写成分量形式^[1]：

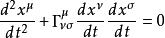其中，

分别为测地线的仿射参数和该坐标系下的克氏符。

测地线方程是一个二阶微分方程组，由于各未知函数及其一阶导数在各个方程中互相耦合，求解并不简单。但是如果时空有足够数量的Killing矢量场，那么就可以利用测地线的切矢和Killing矢量场的内积在测地线上为常数的性质把测地线方程化为一阶微分方程求解。

通过爱因斯坦场方程确定时空度规后就可以解测地线方程来得到自由粒子的运动轨迹。广义相对论最初的观察结果验证日食的光偏折的理论计算，便是爱因斯坦求解史瓦西时空下的测地线方程，利用其一级近似得出的结论。