位移

中文名位移

表达式 ΔX=X2-X1(末位置减初位置)

适用领域范围运动学

目录导航

定义

位移（displacement）质点的位置变动，用连接先后两位置的有向线段表示，如图所示，在瞬时 t质点位于 Q点，瞬时 t+△ t位于 Q′点，则矢量表示质点从 t时刻开始在△ t时间间隔内的位移。它等于 Q′点的矢径与 Q点的矢径之差，即

△ r= r（ t+△t）－ r（ t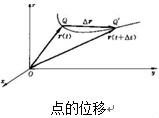）。位移

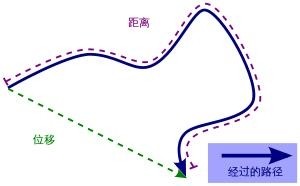
与此同时，质点在△ t时间间隔内由 Q点沿轨迹曲线运动到 Q′，所经过的路程是弧长（标量）。因此，位移和路程是两个不同的概念。当△ t很小，位移矢量的模和路程的差为高阶小量；当△ t→0，两者相等。 ^[1]

计算公式

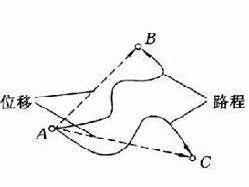
物体在某一段时间内，如果由初位置移到末位置，则由初位置到末位置的有向线段叫做位移。它的大小是运动物体初位置到末位置的直线距离；方向是从初位置指向末位置。位移只与物体运动的始末位置有关，而与运动的轨迹无关。如果质点在运动过程中经过一段时间后回到原处，那么，路程不为零而位移则为零。

位移ΔX=X2-X1(末位置减初位置) 要注意的是位移是直线距离，不是路程。

在国际单位制（SI）中，位移的主单位为：米。此外还有：厘米、千米等。匀变速运动的位移公式：x =v0t+1 /2· at^2

匀变速运动速度与位移的推论： x=Vot+½at²

注：v0指初速度vt指末速度

各项关系

位移方向与速度方向

位移速度方向与位移方向没有直接关系，只有在没有返回（即向着一个方向运动）的直线运动中，速度的方向与位移的方向一定是相同。除此之外，速度方向与位移方向可能相同，也可能不同。例如，在竖直上抛运动中，物体上升时，速度方向（向上）与位移方向（向上）相同，下落过程中在落回抛出点前速度方向（向下）与位移方向（向上）相反，若过抛出点后还可以继续下落，则此后速度方向（向下）又与位移方向（向下）相同。因此要具体情况具体判断。

在曲线运动中，速度方向与位移方向大都不同。因为速度方向为轨迹的切线方向，与轨迹上任意两点的连线（位移）方向多数成不为零的角。

位移方向由运动的起点（你所选择的运动的开始点）指向运动的终点（即末时刻物体所在的点，起点只有一个，而末时刻则可以由问题确定，对应不同的时间段）。例如上述竖直上抛运动，起点是物体的抛出点，而终点则要看问题所给时间的长短，因为可以将整个运动过程分成几段。

位移向量与路径距离

在工业中，特别是受压和受热设备经常会用到“位移”概念，此时的位移，主要是指设备制定部位相对受压、受热、泄压、受冷之前的相对位置量的变化，通常用轴向位移、径向位移、膨胀指数 ^[2] 等术语表示。

区别联系

项目		位移	路程
区别	物理意义	是一条有向线段，表示质点的位置变化	表示物体轨迹运动的长度。
区别	方向性	（1）是矢量，有大小和方向。（2）由起始位置到末位置的方向为位移的方向。（3）这一矢量线段的长为位移的大小。（4）遵守平行四边形定则。	（1）是标量，只有大小，没有方向。（2）物体运动轨迹的长短，即为路程的大小。（3）遵从算术计算
联系	（1）都是长度单位，国际单位都是米(m)。（2）都是描述质点运动的物理量。（3）同一运动过程的路程大小，不小于位移大小；在单向直线运动中，位移大小等于路程。

举例说明

项目		位移	路程
区别	物理意义	是一条有向线段，表示质点的位置变化	表示物体轨迹运动的长度。
区别	方向性	（1）是矢量，有大小和方向。（2）由起始位置到末位置的方向为位移的方向。（3）这一矢量线段的长为位移的大小。（4）遵守平行四边形定则。	（1）是标量，只有大小，没有方向。（2）物体运动轨迹的长短，即为路程的大小。（3）遵从算术计算
联系	（1）都是长度单位，国际单位都是米(m)。（2）都是描述质点运动的物理量。（3）同一运动过程的路程大小，不小于位移大小；在单向直线运动中，位移大小等于路程。