- 常值函数

常值函数
常值函数简介
定义
把常量![]() (
(![]() 为常数)定义为函数,通常是这么理解的:不论自变量
为常数)定义为函数,通常是这么理解的:不论自变量![]() 取什么样的实数值,因变量
取什么样的实数值,因变量![]() 恒取常值
恒取常值![]() ,所以常值函数
,所以常值函数![]() 的定义域
的定义域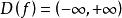 ,值域
,值域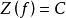 。它的图像是一条平行于
。它的图像是一条平行于![]() 轴并通过点
轴并通过点![]() 在
在![]() 轴上截距为
轴上截距为![]() 的直线(如图1所示)。常值函数的特点是不显含自变量且不存在反函数[1]。
的直线(如图1所示)。常值函数的特点是不显含自变量且不存在反函数[1]。
周期性
常值函数是一个周期函数。因对于任何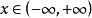 和实数
和实数![]() ,
,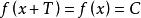 ,但并无最小正周期[1]。
,但并无最小正周期[1]。
导数
常值函数![]() (
(![]() 为常数)的导数
为常数)的导数![]() 。
。
证:对于函数![]() ,当自变量在任意点
,当自变量在任意点![]() 处取改变量
处取改变量![]() 时,
时,![]() 恒成立[2]。
恒成立[2]。
于是
![]() 所以
所以
![]()
常值函数因变量与自变量
常值函数因变量是固定的,即无论自变量取什么值其函数值(因变量)都不会发生变化。因此,实际上常值函数也有自变量,例如![]() 也可以写成
也可以写成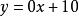 。在没有任何其它限制的情况下,
。在没有任何其它限制的情况下,![]() 可以取任何值,即全体实数。
可以取任何值,即全体实数。
在部分文献中,将常值函数视为0次函数,即![]() 当
当![]() 时,在
时,在![]() 的情况下,恒等于1。但由于0次幂要求
的情况下,恒等于1。但由于0次幂要求![]() ,而常数函数允许
,而常数函数允许![]() ,所以也有些文献不赞成将常数函数视为0次函数。
,所以也有些文献不赞成将常数函数视为0次函数。
周期函数简介
定义
对于函数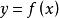 ,若存在常数
,若存在常数![]() ,使得f(x+T) = f(x),则函数
,使得f(x+T) = f(x),则函数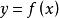 称为周期函数,T称为此函数的周期。
称为周期函数,T称为此函数的周期。
性质
性质1:若T是函数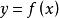 的任意一个周期,则T的相反数(-T)也是
的任意一个周期,则T的相反数(-T)也是![]() 的周期。
的周期。
性质2:若T是函数![]() 的周期,则对于任意的整数n(n≠0),nT也是
的周期,则对于任意的整数n(n≠0),nT也是![]() 的周期。
的周期。
性质3:若![]() 都为函数
都为函数![]() 的周期,且
的周期,且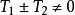 ,则
,则![]() 也是
也是![]() 的周期。
的周期。
周期性
在函数![]() 的周期的集合中,我们称其正数者为函数
的周期的集合中,我们称其正数者为函数![]() 的正周期,称其负数者为函数
的正周期,称其负数者为函数![]() 的负周期。若所有正周期中存在最小的一个,则我们称之为函数
的负周期。若所有正周期中存在最小的一个,则我们称之为函数![]() 的最小正周期,记作T*。
的最小正周期,记作T*。
补充:常值函数无单调性。

-
1641函数信号发生器
2025-09-21 22:35:52 查看详情


 求购
求购










