- 有效除子

有效除子
定义
除子(divisor)亦称韦伊除子,是研究代数簇的重要工具之一,指不可约簇X上余维数为1的不可约子簇的代数和。具体地,若D表示X中不含于X的奇异轨迹之中且余维数为1的不可约子簇的全体, 表示以D为基的自由阿贝尔群,则
表示以D为基的自由阿贝尔群,则 中的元称为除子。设
中的元称为除子。设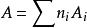 是一个除子,
是一个除子,![]() 是不可约子簇,若所有的
是不可约子簇,若所有的![]() ,则称A为有效除子,称
,则称A为有效除子,称![]() 为素除子。例如,若X是余维数1正则的(即X的所有一维局部环都是正则环)射影簇,A是X上的素除子,则
为素除子。例如,若X是余维数1正则的(即X的所有一维局部环都是正则环)射影簇,A是X上的素除子,则![]() 是一个离散赋值环。若f是X上的非零有理函数,则对
是一个离散赋值环。若f是X上的非零有理函数,则对![]() 的赋值
的赋值 是个整数,且除了有限多个A之外,
是个整数,且除了有限多个A之外,![]() 。因此,可以定义f的除子
。因此,可以定义f的除子
![]() 这种除子称为主除子。若两个除子
这种除子称为主除子。若两个除子![]() 的差等于一个主除子,即
的差等于一个主除子,即 则称D和D′是线性等价的。
则称D和D′是线性等价的。 关于线性等价的商群称为X的除子类群,记为
关于线性等价的商群称为X的除子类群,记为![]() [1]。
[1]。
详细介绍
定义设![]() 是一个一维代数函数域,
是一个一维代数函数域,![]() 的任何一个离散赋值环称为一个素除子,由素除子全体所生成的自由Abel群称为
的任何一个离散赋值环称为一个素除子,由素除子全体所生成的自由Abel群称为![]() 的除子群,记作
的除子群,记作 ,其中的元素称为除子[2]。
,其中的元素称为除子[2]。
设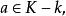 按照一维函数域的定义,k在K中代数封闭,故
按照一维函数域的定义,k在K中代数封闭,故![]() 是k上的超越元,因此K是
是k上的超越元,因此K是![]() 的有限扩张,令
的有限扩张,令 即环
即环![]() 在它的素理想
在它的素理想![]() 的局部化,则A是
的局部化,则A是![]() 的一个离散赋值环,它在K中只有有限多个扩张,这表明
的一个离散赋值环,它在K中只有有限多个扩张,这表明![]() 只有有限多个不等价的离散赋值v满足
只有有限多个不等价的离散赋值v满足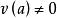 。
。
定义把![]() 中的素除子全体所组成的集合记作
中的素除子全体所组成的集合记作![]() ,对任何
,对任何![]() ,记
,记![]() 为P所对应的标准赋值.对于
为P所对应的标准赋值.对于![]() ,除子
,除子 称为一个主除子。主除子全体形成
称为一个主除子。主除子全体形成 的一个子群,
的一个子群, 关于这个子群的商群称为
关于这个子群的商群称为![]() 的Picard群,记作
的Picard群,记作 ,Picard群有时也叫做除子类群,记作
,Picard群有时也叫做除子类群,记作 属于同一个等价类里的两个除子
属于同一个等价类里的两个除子![]() 称为是线性等价的,记为
称为是线性等价的,记为 。
。
对任意![]() 它的剩余类域k'是k的有限扩张,记
它的剩余类域k'是k的有限扩张,记 称为P的剩余类域指数。设
称为P的剩余类域指数。设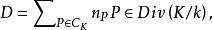 其中
其中 ,则定义
,则定义 为D在点P的阶,定义
为D在点P的阶,定义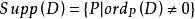 ,又定义
,又定义 为D的次数,记作deg(D)。除子
为D的次数,记作deg(D)。除子 和
和 分别叫做D的正的部分和负的部分。如果
分别叫做D的正的部分和负的部分。如果![]() 对每个
对每个![]() 成立,则称D为一个有效除子。若
成立,则称D为一个有效除子。若 且
且![]() 是有效除子,则记
是有效除子,则记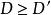 ,特别不等式
,特别不等式![]() 相当于说D是有效除子。设
相当于说D是有效除子。设 ,定义
,定义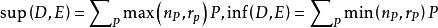
设C是代数闭域k上的光滑射影曲线,则C的除子、Picard群Pic(C)等概念都定义为C的函数域K(C)的相应概念[2]。

-
雪铁龙C4 更加顺畅有效
2025-09-21 09:39:44 查看详情 -
试驾雪铁龙云逸 更加顺畅有效
2025-09-21 09:39:44 查看详情 -
雪铁龙C6ORIGINS百年臻享型怎么样 更加顺畅有效
2025-09-21 09:39:44 查看详情 -
东风雪铁龙C4L车内空气质量超豪车 更加顺畅有效
2025-09-21 09:39:44 查看详情 -
雪铁龙C3 更加顺畅有效
2025-09-21 09:39:44 查看详情 -
东风雪铁龙云逸上市点评解析 更加顺畅有效
2025-09-21 09:39:44 查看详情


 求购
求购




