- 独立性

独立性
两个事件的独立性
定义1
若![]() 两事件满足等式
两事件满足等式
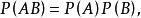 则称事件A与B相互独立。[1]
则称事件A与B相互独立。[1]
注意点
(1)概率为零的事件与任何事件相互独立;
(2) 当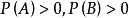 时,
时,![]() 相互独立与
相互独立与![]() 互不相容不能同时成立,它们是完全不同的两个概念:
互不相容不能同时成立,它们是完全不同的两个概念:![]() 相互独立是从概率的角度来考虑的,
相互独立是从概率的角度来考虑的,![]() 互不相容是从事件本身来考虑的。
互不相容是从事件本身来考虑的。
性质定理
定理1设![]() 是两事件。且
是两事件。且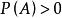 ,若
,若![]() 相互独立。则
相互独立。则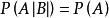 ,反之亦然。
,反之亦然。
定理2若事件A与B相互独立,则![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() 也相互独立。
也相互独立。
证明:这里只证明![]() 与
与![]() 相互独立。
相互独立。
由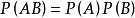 ,
,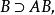 得
得
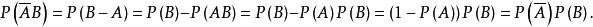
所以![]() 与
与![]() 相互独立。[1]
相互独立。[1]
有限个事件的独立性
三个事件相互独立
设![]() 为3个事件,如果满足等式
为3个事件,如果满足等式
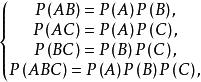 则称事件
则称事件![]() 相互独立。
相互独立。
对![]() 个事件的独立性,可类似写出其定义。[1]
个事件的独立性,可类似写出其定义。[1]
n个事件相互独立
一般地,设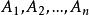 是
是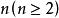 个事件,如果对于其中任意2个,任意3个,...,任意
个事件,如果对于其中任意2个,任意3个,...,任意![]() 个事件的积事件的概率,都等于各事件概率之积,则称
个事件的积事件的概率,都等于各事件概率之积,则称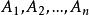 相互独立。
相互独立。
两两独立
设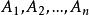 是
是![]() 个事件,若其中任意两个事件之间均相互独立,则称
个事件,若其中任意两个事件之间均相互独立,则称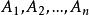 两两独立。
两两独立。
注:相互独立一定两两独立、两两独立不一定相互独立。
例题:如果将一枚硬币抛掷两次,观察正面H和反面T的出现情况,则此时样本空间为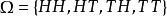 ,令
,令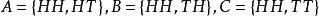 。
。
则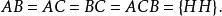
故有
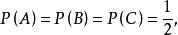
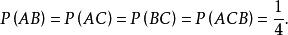 由定义1知,
由定义1知,![]() 任意两个事件都是相互独立的,但是
任意两个事件都是相互独立的,但是
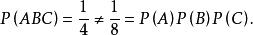 也就是说
也就是说![]() 两两独立,并不相互独立。[1]
两两独立,并不相互独立。[1]
相互独立性的性质
性质1
若事件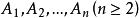 相互独立,则其中任意
相互独立,则其中任意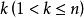 个事件也相互独立。
个事件也相互独立。
由独立性定义可直接推出性质1。 ’
性质2
若n个事件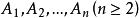 相互独立,则将
相互独立,则将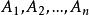 中任意
中任意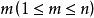 个事件换成它们的对立事件,所得的n个事件仍相互独立。
个事件换成它们的对立事件,所得的n个事件仍相互独立。
从直观上看是显然的,对![]() 时,定理2已作证明,一般情况叮利用数学归纳法证之,此处略。[1]
时,定理2已作证明,一般情况叮利用数学归纳法证之,此处略。[1]
与相关性的关系
假设随机变量X、Y的相关系数存在。如果X和Y相互独立,那么X、Y不相关。反之,若X和Y不相关,X和Y却不一定相互独立。不相关只是就线性关系来说的,而相互独立是就一般关系而言的。[2]
例题解析
例1有两门高射炮独立地射击一架敌机,设甲炮击中敌机的概率为0.8,乙炮击中敌机的概率为0.7,试求敌机被击中的概率。[1]
解:设A={甲炮击中敌机},B={乙炮击中敌机},则A U B={敌机被击中},由题意知,P(A)=0.8,P(B)=0.7,由于A,B相互独立。故
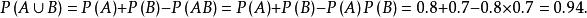
例2有甲、乙两批种子,发芽率分别为0.8和0.7,并假设每批种子发芽与否是相互独立的,从两批种子中各随机地抽取一粒,求:
(1)两粒都能发芽的概率;
(2)至少有一粒种子能发芽的概率;
(3)恰好有一粒种子能发芽的概率。
解:设A={取自甲批种子中的某粒种子能发芽},B={取自乙批种子中的某粒种子能发芽},则所求的概率分别为: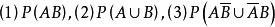 。
。
由于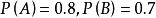 ,且
,且![]() 相互独立,故有:
相互独立,故有:
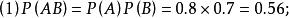
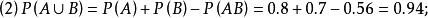
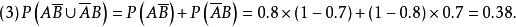
例3甲、乙两人进行网球比赛。每局甲胜的概率为p,且![]() .试问对甲而言,采用三局二胜制有利,还是采用五局三胜制有利?设各局胜负相互独立。
.试问对甲而言,采用三局二胜制有利,还是采用五局三胜制有利?设各局胜负相互独立。
解:采用三局二胜制,甲最终获胜,其胜局的情况是:“甲甲”或“乙甲甲”或“甲乙甲”,而这三种结局互不相容,于是由独立性得甲最终获胜的概率为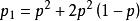 。
。
采用五局三胜制,甲最终获胜,至少需比赛3局(可能赛3局.也可能赛4局或5局),且最后一局必须是甲胜,而前面甲需胜二局。例如.共赛4局,则甲的胜局情况是:“甲乙甲甲”、“乙甲甲甲”、“甲甲乙甲”、且这三种结局互不相容,由独立性得甲最终获胜的概率为:
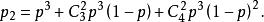 于是,
于是,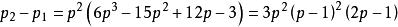 。
。
当![]() 时,
时,![]() ,即对甲来说采用五局三胜制较为有利;当
,即对甲来说采用五局三胜制较为有利;当![]() 时,
时, 即两种赛制甲、乙最终获胜的概率相同。[1]
即两种赛制甲、乙最终获胜的概率相同。[1]
上面这个例子所涉及的随机试验只有两种可能的结果:甲胜或甲输,且试验在相同条件下可独立重复地进行,在每次试验中甲胜的概率都是相同的,具有这种特征的概型就是伯努利概型。[1]

-
吉利嘉际白金款PHEV售价上调 吉利或新建电动车独立公司
2025-02-06 12:17:31 查看详情 -
吉利星越L 吉利或新建电动车独立公司
2025-02-06 12:17:31 查看详情 -
吉利或新建电动车独立公司 将于本月底上市
2025-02-06 12:17:31 查看详情 -
吉利豪越L官图曝光 吉利或新建电动车独立公司
2025-02-06 12:17:31 查看详情 -
吉利或新建电动车独立公司 2025年换电站将超5000座
2025-02-06 12:17:31 查看详情


 求购
求购




