基础解系

基础解系(3)对于m个方程、n个未知数的齐次线性方程组，系数矩阵记为A，其秩记为r(A)，齐次线性方程组总有零解，不存在无解的情况，且其有非零解的等价条件为，即系数矩阵中的列向量线性相关。而且齐次线性方程组的解向量的线性组合仍然是该线性方程组的解。证明如下：

设是的两个不相等的解向量，即有：

令，其中为任意实数，即称为的线性组合，且有：

即可得，也是的解。

把由齐次线性方程组的解所构成的集合称为解空间，它的维数为。 该解空间中的一组基就成为该线性方程组的一组基础解系。换句话说，基础解系是由个线性无关的解向量构成的，基础解系的解向量个数是确定的，但解向量是不确定的，只要两两之间线性无关即可。基础解系的任意线性组合构成了该齐次线性方程组的一般解，也称通解^[1]。

要证明一组向量为齐次线性方程组的基础解系时，必须满足以下三条：

（1）这组向量是该方程组的解；

（2）这组向量必须是线性无关组，即基础解系各向量线性无关；

（3）方程组的任意解均可由基础解系线性表出，即方程组的所有解都可以用基础解系的量来表示。

另外，这组向量所含向量的个数，其中是未知量的个数，即系数矩阵的列数^[1]

求法一：先求出齐次或非齐次线性方程组的一般解，即先求出用自由未知量表示独立未知量的一般解的形式，然后将此一般解改写成向量线性组合的形式，则以自由未知量为组合系数的解向量均为基础解系的解向量。由此易知，齐次线性方程组中含几个自由未知量，其基础解系就含几个解向量^[2]。

求法二：先确定自由未知量，不妨设AX=b的系数矩阵A的秩为r，并假设A经过初等行变换化为如下形式：

则AX=0分别可化为如下的同解方程组：

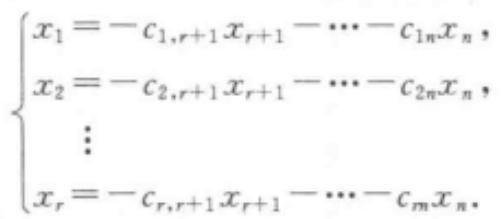
令自由未知量xr+1，xr+2，……，xn分别取n－r组数[1,0,...,0],[0,1,...,0],...,[0,0,0,...,1]，将其带入方程组，分别带入x1，x2，……，xr分别取n－r组数，这样就得到基础解系所含的n一r个线性无关的解，即

基础解系【例题1】：

已知齐次线性方程组的一组基础解系为，则下列结论是否正确？

a.也为的一组基础解系。

b.向量组能被向量组线性表出，则也是的基础解系。

c.向量组与向量组可以互相线性表出，则也是的基础解系。

d.向量组与向量组是等价的向量组，则也是的基础解系。

【解析】：

a.正确。 首先因是线性方程组的3个解向量，它们的线性组合也是的解。再证它们是线性无关的。证明方法有很多种，最简单的方法是：设，矩阵的列秩等于3，而通过列初等变换可把化为，（初等变换不改变矩阵的秩），所以的列秩也为3. 列向量组为的3个线性无关的解向量，满足前面提出的3条（见证明），所以它们构成的一组基础解系。

b.不正确。因为能被线性表出，根据定理，，这不能保证（例如，则线性相关），即有可能成为的一组线性相关解，故不能构成的一组基础解系。

c.正确。两组向量可以互相线性表出，故，且有满足，即它们为的3个线性无关解，故构成的一组基础解系。

d.不正确。因为的个数为4，故不能构成的基础解系，实际上，因为两组向量等价，故等秩，向量组是线性相关的。^[1]