- 酉矩阵

酉矩阵
定义
若一![]() 行
行![]() 列的复数矩阵
列的复数矩阵![]() 满足:
满足:
![]()
其中,![]() 为
为![]() 的共轭转置,
的共轭转置,![]() 为
为![]() 阶单位矩阵,则
阶单位矩阵,则![]() 称为酉矩阵。[1]
称为酉矩阵。[1]
判别准则
一个简单的充分必要判别准则是:
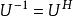
或者说,酉矩阵的共轭转置和它的逆矩阵相等。[1]
性质和应用
酉矩阵的相关性质:
设有矩阵![]() ,则
,则
(1)若![]() 是酉矩阵,则
是酉矩阵,则![]() 的逆矩阵也是酉矩阵;
的逆矩阵也是酉矩阵;
(2)若![]() 是酉矩阵,则
是酉矩阵,则![]() 和
和![]() 也是酉矩阵;
也是酉矩阵;
(3)若![]() 是酉矩阵,则
是酉矩阵,则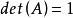 ;
;
(4)![]() 是酉矩阵的充分必要条件是,它的
是酉矩阵的充分必要条件是,它的![]() 个列向量是两两正交的单位向量。
个列向量是两两正交的单位向量。
酉方阵在量子力学中有着重要的应用。酉等价是标准正交基到标准正交基的特殊基变换。[1]
广义酉矩阵
定义
假定![]() 表示所有m×n复矩阵的集合,
表示所有m×n复矩阵的集合,![]() 表示所有n阶复可逆矩阵的集合,
表示所有n阶复可逆矩阵的集合,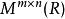 表示所有m×n实矩阵的集合,
表示所有m×n实矩阵的集合,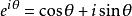 ,(
,(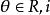 表示纯虚数)。
表示纯虚数)。
定义1,设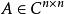 ,若存在
,若存在![]() 使
使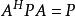 ,则称A为n阶P-广义酉矩阵;记为
,则称A为n阶P-广义酉矩阵;记为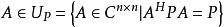 。
。
性质
定理1,若![]() 相似于一个酉矩阵U,则A是n阶P-广义酉矩阵。
相似于一个酉矩阵U,则A是n阶P-广义酉矩阵。
推论1,若![]() 相似于一个酉矩阵U,则
相似于一个酉矩阵U,则![]() 与
与![]() 相似。
相似。
定理2,已知A可对角化,则A为n阶P-广义酉矩阵的充分必要条件是A相似于一个酉矩阵。
定理3,已知A是n阶P-广义酉矩阵。如果λ≠0是A的特征值,那么1/λ是![]() 的特征值;当A为实矩阵时,1/λ也是A的特征值。
的特征值;当A为实矩阵时,1/λ也是A的特征值。
定理4,若A为广义P-酉矩阵,则A是广义PH-酉矩阵。



 求购
求购
