- 拓扑关系

拓扑关系
定义
拓扑关系是指图形元素之间相互空间上的连接、邻接关系并不考虑具体位置。这种拓扑关系是由数字化的点、线、面数据形成的以用户的查询或应用分析要求进行图形选取、叠合、合并等
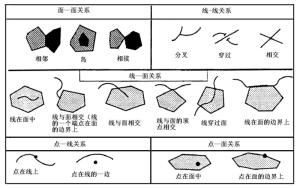 拓扑关系(拓扑邻接、拓扑关联、拓扑包含)
拓扑关系(拓扑邻接、拓扑关联、拓扑包含)
操作。建立空间要素之间的拓扑关系属于地图整饰。
点、线、面等实体之间的空间联系,如连通性、邻接性、包含关系等。连通性是指对线段连接关系的判别;可以用在每个结点上汇集的线段的列表来表示。邻接性通常指多边形之间的邻接关系;包含关系通常指多边形包含点或包含其他的多边形。
拓扑
是将各种物体的位置表示成 抽象位置。在网络中,拓扑形象地描述了网络的安排和配置,包括各种结点和结点的相互关系。拓扑不关心事物的细节也不在乎什么相互的比例关系,只将讨论范围内的 事物之间的相互关系表示出来,将 这些事物之间的关系通过图表示出来。
类别
非拓扑属性
两点之间的距离; 一个点指向另一个点的方向;弧段的长度;一个区域的周长;一个区域的面积。
拓扑属性
一个点在一个弧段的端点; 一个简单弧段不会自相交; 一个点在一个区域的边界上;一个点在一个区域的内部; 一个点在一个区域的外部; 一个点在一个环的内部; 一个简单面是一个连续的面 。
拓扑数据结构
1.拓扑结构的基本元素
①拓扑线段(arc)
该线段中间不与其它线段存在联系。
②结点(node)
拓扑线段的两个端点,分别为首结点、尾结点
③多边形(poly)
由数条拓扑线段连接而成
拓扑数据举例:
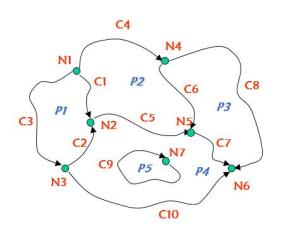 拓扑数据举例
拓扑数据举例
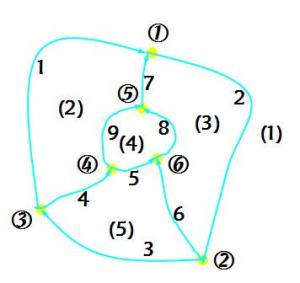
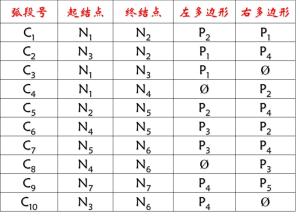
2.拓扑关系表的建立
结点编码:①②③④⑤⑥
线段编码:1 2 3 4 5 6 7 8 9
多边形编码:(1)(2)(3)(4)(5)
常见拓扑结构
星型结构
星型结构是以一个节点为中心的处理系统,各种类型的入网机器均与该中心节点有物理链路直接相连。
星型结构的优点是结构简单、建网容易、控制相对简单。其缺点是属集中控制,主节点负载过重,可靠性低,通信线路利用率低。
总线结构
总线结构是比较普遍采用的一种方式,它将所有的入网计算机均接入到一条通信线上,为防止信号反射,一般在总线两端连有终结器匹配线路阻抗。
总线结构的优点是信道利用率较高,结构简单,价格相对便宜。缺点是同一时刻只能有两个网络节点相互通信,网络延伸距离有限,网络容纳节点数有限。在总线上只要有一个点出现连接问题,会影响整个网络的正常运行。在局域网中多采用此种结构。
环型结构
环型结构是将各台连网的计算机用通信线路连接成一个闭合的环。
环型拓扑是一个点到点的环型结构。每台设备都直接连到环上,或通过一个接口设备和分支电缆连到环上。 在初始安装时,环型拓扑网络比较简单。随着网上节点的增加,重新配置的难度也增加,对环的最大长度和环上设备总数有限制。可以很容易地找到电缆的故障点。受故障影响的设备范围大,在单环系统上出现的任何错误,都会影响网上的所有设备。
树型结构
星型网络拓扑结构的一种扩充便是星行树,如左图所示。每个Hub与端用户的连接仍为星型,Hub的级连而形成树。然而,应当指出,Hub级连的个数是有限制的,并随厂商的不同而有变化。
树型结构是分级的集中控制式网络,与星型相比,它的通信线路总长度短,成本较低,节点易于扩充,寻找路径比较方便,但除了叶节点及其相连的线路外,任一节点或其相连的线路故障都会使系统受到影响。
适用场合:只适用于低速、不用阻抗控制的信号,比如在没有电源层的情况下,电源的布线就可以采用这种拓扑。
网状结构
网状结构分为全连接网状和不完全连接网状两种形式。全连接网状中,每一个节点和网中其它节点均有链路连接。不完全连接网中,两节点之间不一定有直接链路连接,它们之间的通信,依靠其它节点转接。这种网络的优点是节点间路径多,碰撞和阻塞可大大减少,局部的故障不会影响整个网络的正常工作,可靠性高;网络扩充和主机入网比较灵活、简单。但这种网络关系复杂,建网不易,网络控制机制复杂。广域网中一般用不完全连接网状结构。
混合型拓扑
就是两种或两种以上的拓扑结构同时使用。
优点:可以对网络的基本拓扑取长补短。 缺点:网络配置难度大。
蜂窝拓扑结构
蜂窝拓扑结构是无线局域网中常用的结构。它以无线传输介质(微波、卫星、红外等)点到点和多点传输为特征,是一种无线网,适用于城市网、校园网、企业网。
由来
哥尼斯堡七桥问题折叠
在数学上,关于哥尼斯堡七桥问题、多面体欧拉定理、四色问题等都是拓扑学发展史的重要问题。哥尼斯堡七桥问题哥尼斯堡(今俄罗斯加里宁格勒)是东普鲁士的首都,普莱格尔河横贯其中。十八世纪在这条河上建有七座桥,将河中间的两个岛和河岸联结起来。人们闲暇时经常在这上边散步,一天有人提出:能不能每座桥都只走一遍,最后又回到原来的位置。这个看起来很简单又很有趣的问题吸引了大家,很多人在尝试各种各样的走法,但谁也没有做到。看来要得到一个明确、理想的答案还不那么容易。
1736年,有人带着这个问题找到了当时的大数学家欧拉,欧拉经过一番思考,很快就用一种独特的方法给出了解答。欧拉把这个问题首先简化,他把两座小岛和河的两岸分别看作四个点,而把七座桥看作这四个点之间的连线。那么这个问题就简化成,能不能用一笔就把这个图形画出来。经过进一步的分析,欧拉得出结论——不可能每座桥都走一遍,最后回到原来的位置。并且给出了所有能够一笔画出来的图形所应具有的条件。这是拓扑学的“先声”。
多面体的欧拉定理折叠
在拓扑学的发展历史中,还有一个着名而且重要的关于多面体的定理也和欧拉有关。这个定理内容是:如果一个凸多面体的顶点数是v、棱数是e、面数是f,那么它们总有这样的关系:f+v-e=2。
根据多面体的欧拉定理,可以得出这样一个有趣的事实:只存在五种正多面体。
它们是正四面体、正六面体、正八面体、正十二面体、正二十面体。
四色猜想折叠
著名的“四色问题”也是与拓扑学发展有关的问题。四色问题又称四色猜想,是世界近代三大数学难题之一。 四色猜想的提出来自英国。1852年,毕业于伦敦大学的弗南西斯·格思里来到一家科研单位搞地图着色工作时,发现了一种有趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共同边界的国家都被着上不同的颜色。”
1872年,英国当时最着名的数学家凯利正式向伦敦数学学会提出了这个问题,于是四色猜想成了世界数学界关注的问题。世界上许多一流的数学家都纷纷参加了四色猜想的大会战。1878~1880年两年间,著名律师兼数学家肯普和泰勒两人分别提交了证明四色猜想的论文,宣布证明了四色定理。但后来数学家赫伍德以自己的精确计算指出肯普的证明是错误的。不久,泰勒的证明也被人们否定了。于是,人们开始认识到,这个貌似容易的题目,其实是一个可与费马猜想相媲美的难题。
进入20世纪以来,科学家们对四色猜想的证明基本上是按照肯普的想法在进行。电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了对四色猜想证明的进程。1976年,美国数学家阿佩尔与哈肯在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿次判断,终于完成了四色定理的证明。不过不少数学家并不满足于计算机取得的成就,他们认为应该有一种简捷明快的书面证明方法。
上面的几个例子所讲的都是一些和几何图形有关的问题,但这些问题又与传统的几何学不同,而是一些新的几何概念。这些就是“拓扑学”的先声。

-
大众TALAGON/皇冠陆放领衔 与三家公司建立合作关系
2025-09-20 23:56:01 查看详情 -
长城与SQ集团汇鸿汽车达成合作伙伴关系 将于上海车展首发亮相
2025-09-20 23:56:01 查看详情 -
大众途锐级别全新电动车正在研发 与三家公司建立合作关系
2025-09-20 23:56:01 查看详情 -
长城与SQ集团汇鸿汽车达成合作伙伴关系 诠释独特设计美学
2025-09-20 23:56:01 查看详情 -
大众ID.4原型车实车曝光 与三家公司建立合作关系
2025-09-20 23:56:01 查看详情 -
全新大众Passat旅行版最新谍照 与三家公司建立合作关系
2025-09-20 23:56:01 查看详情 -
长城与SQ集团汇鸿汽车达成合作伙伴关系 将于上海车展亮相
2025-09-20 23:56:01 查看详情 -
长城与SQ集团汇鸿汽车达成合作伙伴关系 相关内部人事透露
2025-09-20 23:56:01 查看详情


 求购
求购



