- 网络流

网络流
定义
假设 是一个有限的有向图,它的每条边 都有一个非负值实数的容量。如果,我们假设 。我们区别两个顶点:一个源点 和一个汇点 。一道网络流是一个对于所有结点 和 都有以下特性的实数函数 :
| 容量限制(Capacity Constraints): | 一条边的流不能超过它的容量。 |
| 反对称(Skew Symmetry): | |
| 流守恒(Flow Conservation): | 除非 |
即流守恒意味着: ,对每个顶点
注意 是由
到
的净流。如果该图代表一个实质的网络,由
到
有4单位的实际流及由
到
有3单位的实际流,那么
及
。
基本上,我们可以说,物理网络的网络流是从 s = 出发的流
边的剩余容量(residual capacity)是 。这定义了以
表示的剩余网络(residual network),它显示可用的容量的多少。留意就算在原网络中由
到
没有边,在剩余网络仍可能有由
到
的边。因为相反方向的流抵消,减少由
到
的流等于增加由
到
的流。增广路(augmenting path)是一条路径
,而
、
及
,这表示沿这条路径发送更多流是可能的。当且仅当剩余网络
没有增广路时处于最大流。
因此如下使用图 G 创建 :
=
的顶点
定义如下的
=
的边
对每条边
若
,创建容量为
的前向边
。
若
,创建容量为
的后向边
。
这个概念用在计算流量网的最大流的Ford–Fulkerson算法中。
有时需要对有多于一个源点的网络,于是就引入了图的超源点。 这包含了一个与无限容量的边连接的每个源点,以作为一个整体源点。汇点也有类似的构造称作超汇点。
例子
| 容量限制(Capacity Constraints): | 一条边的流不能超过它的容量。 |
| 反对称(Skew Symmetry): | |
| 流守恒(Flow Conservation): | 除非 |
应用
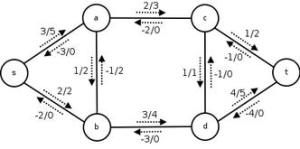 一个显示了流及容量的流网络。
一个显示了流及容量的流网络。
在右边可以看到一个有以标示的源点、以
标示的汇点及4个额外结点的流网络。流及容量以
显示。注意网络怎样保证斜对称、容量限制及流守恒。由
到
的总流量为5,由此可简单地观察到源于
的所有向外流是5,也就是汇于
的向内流。我们知道在其它结点中没有任何流出现或消失。
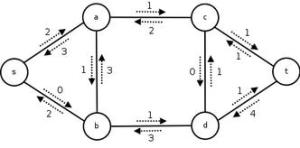 上面的流网络的剩余网络,显示了剩余容量。
上面的流网络的剩余网络,显示了剩余容量。
在下面你可以看到对既定的流的剩余网络。注意某些边的剩余容量是正数而原来的容量是零,如边。这道流不是一道最大流。沿路径
、
及
还有可用的容量,也就是扩张路径。第一条路径的剩余容量是
。注意扩张路径
在原来的网络中并不存在,但你可以沿它发送流,因此仍是一道正当的流。
假如这是一个真实的网络,由到
的2单位的流及由
到
的1单位的流事实上可能存在,但我们只维持净流。

-
第十八届中国网络媒体论坛
2025-11-02 16:57:52 查看详情 -
北京大学网络教育学院
2025-11-02 16:57:52 查看详情 -
2018中国网络媒体论坛共识
2025-11-02 16:57:52 查看详情 -
网络表演经营活动管理办法
2025-11-02 16:57:52 查看详情


 求购
求购








