- 凹面镜成像

凹面镜成像
具体原理
特点
一个凹面镜的图解,显示出焦点、焦距、曲率中心、主轴等等。凹面镜或汇聚镜会将反射的光线像内偏折(永远朝像入射光源)。不同于凸面镜,凹面镜会因为物体与镜面本身距离的不同,而呈现不同的影像。
用途
凹面镜由于是反射成像,不会出现色差,这是任何透镜成像所不能比拟的优势。望远镜的分辨率和物镜的通光口径成正比,而大口径的透镜的制造是极其困难的,利用反射原理制造的凹面镜则易于制造得多。因此,凹面镜常用于制作望远镜。
成像规律
当物距小于焦距时成正立、放大的虚像,物体离镜面越近,像越小。当物距等于一倍焦距时不成像,当物距在一二倍焦距之间时成倒立放大的实像,物体离镜面越远,像越小。当物距等于二倍焦距时成等大倒立的实像。当物距大于2倍焦距时,成倒立、缩小的实像,物体离镜面越远,像越小。成的实像与物体在同侧,成的虚像与物体在异侧。
| S:表示物体与镜面的距离。F:表示曲面镜的焦距。 | 所得影像 | 示意图 |
| S < F(物体在焦点与镜面之间) | 1)虚像2)正像3)放大(比实物大) | 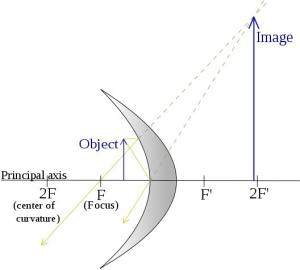 S 〈 F S 〈 F |
| S = F(物体在焦点上) | 1)反射的光线是彼此互相平行不会交会,因此无法成像。2)当S无限接近于F时,影像的位置越接近无限处。而且所得影像可以是实像或者是虚像;可以是正像也可以是反像。这取决于物体靠近焦点的方向到底是从焦点的上方还是下方 |  S = F S = F |
| F < S < 2F(物体在焦点与曲率之间) | 1)实像2)倒置(垂直于主轴)3)放大(比实物大) | 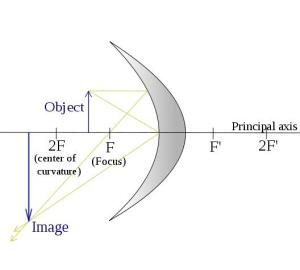 F 〈 S 〈 2F F 〈 S 〈 2F |
| S = 2F(物体在曲率上) | 1)实像2)倒置(垂直于主轴)3)一样大小4)影像形成在曲率上 | 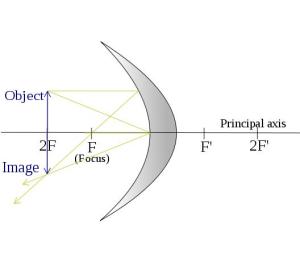 S = 2F S = 2F |
| S > 2F(物体超过了曲率) | 1)实像2)倒置(垂直于主轴)3)缩小(比物体小)4)当S增加,影像逐渐靠近焦点5)当S接近于无穷大时,影像的大小趋向于0,位置无限靠近焦点; |  S 〉 2F S 〉 2F |
实际应用
| S:表示物体与镜面的距离。F:表示曲面镜的焦距。 | 所得影像 | 示意图 |
| S < F(物体在焦点与镜面之间) | 1)虚像2)正像3)放大(比实物大) |  S 〈 F S 〈 F |
| S = F(物体在焦点上) | 1)反射的光线是彼此互相平行不会交会,因此无法成像。2)当S无限接近于F时,影像的位置越接近无限处。而且所得影像可以是实像或者是虚像;可以是正像也可以是反像。这取决于物体靠近焦点的方向到底是从焦点的上方还是下方 |  S = F S = F |
| F < S < 2F(物体在焦点与曲率之间) | 1)实像2)倒置(垂直于主轴)3)放大(比实物大) |  F 〈 S 〈 2F F 〈 S 〈 2F |
| S = 2F(物体在曲率上) | 1)实像2)倒置(垂直于主轴)3)一样大小4)影像形成在曲率上 |  S = 2F S = 2F |
| S > 2F(物体超过了曲率) | 1)实像2)倒置(垂直于主轴)3)缩小(比物体小)4)当S增加,影像逐渐靠近焦点5)当S接近于无穷大时,影像的大小趋向于0,位置无限靠近焦点; |  S 〉 2F S 〉 2F |
形状
数学理论
多数的曲面镜都是球面的外观,因为这是最容易制作,也是最通用的形状。但是球面镜易产生球面像差,平行的光线反射后不能汇聚在单一的焦点上。平行的光线,例如来自非常遥远目标的光,使用抛物面镜可以获得更好的效果,因为抛物面镜汇聚的光点比球面镜的更小。所以我们在研究凹面镜成像时,大多是研究近轴光线,此时可将凹面镜焦点视为球心与中心(光心)连线的中点处。
制镜要点
在数学的论述下,平轴近似,意味着以下的第一近似是将球面反射镜当成抛物面反射镜。一个球面的凹面反射镜的球面反射镜的光矩阵显示如下: C是矩阵的元素,此处 f是光学设计上的焦点。
方块1和方块3的特性是角度的和是π(180°),方块2显示Maclaurin系列第一阶的弧长为。凸球面镜导出的光矩阵和薄透镜是非常相似的。

-
奥迪Q5倒车镜开关安装方法(奥迪Q5倒车镜开关怎么安装)
2025-09-21 11:54:33 查看详情 -
奥迪s5外后视镜折怎么操作(奥迪s5外后视镜折操作的方法)
2025-09-21 11:54:33 查看详情 -
奥迪a6如何调整车内后视镜(奥迪a6调整车内后视镜的教程)
2025-09-21 11:54:33 查看详情 -
奥迪q7如何打开和折叠后视镜(奥迪q7怎样打开和折叠后视镜)
2025-09-21 11:54:33 查看详情 -
奥迪a6汽车倒车镜壳拆卸技巧(奥迪a6汽车倒车镜壳拆卸有什么技巧)
2025-09-21 11:54:33 查看详情 -
奥迪a4l怎么调后视镜(奥迪a4后视镜按钮如何使用)
2025-09-21 11:54:33 查看详情


 求购
求购




