- 黄金分割

黄金分割
数学定义
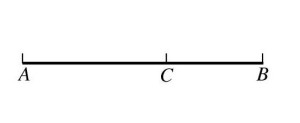
把一条线段分割为两部分,使较大部分与全长的比值等于较小部分与较大的比值,则这个比值即为黄金分割。其比值是(√5-1):2,近似值为0.618,通常用希腊字母Ф表示这个值。[3]
附:黄金分割数前面的32位为:0.6180339887 4989484820 458683436565
 |
||
尺规作图
 |
||
推广拓展
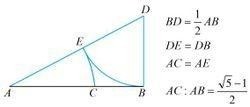 图示1、设已知线段为AB,过点B作BD⊥AB,且BD=AB/2
图示1、设已知线段为AB,过点B作BD⊥AB,且BD=AB/2
2、连结AD
3、 以D为圆心,DB为半径作弧,交AD于E
4、以A为圆心,AE为半径作弧,交AB于C,则点C即为黄金分割点[4]
在一个黄金矩形中,以一个顶点为圆心,矩形的较短边为半径作一个四分之一圆,交较长边于一点,过这个点,作一条直线垂直于较长边,这时,生成的新矩形仍然是一个黄金矩形,这个操作可以无限重复,产生无数个的黄金矩形。[4]
分数与根式
特殊的数列
设![]() 为黄金比,便有
为黄金比,便有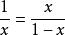 。然后有
。然后有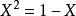 ,
,![]() ,得
,得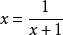 。对等式右边分母中的
。对等式右边分母中的![]() 又以
又以![]() 代替,可得
代替,可得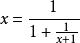 ;以此类推,可得无穷连分数。对等式进行类似的代替,可得无穷连根号。[5]
;以此类推,可得无穷连分数。对等式进行类似的代替,可得无穷连根号。[5]
黄金三角形
设一个数列,它的最前面两个数是1、1,后面的每个数都是它前面的两个数之和。例如:1,1,2,3,5,8,13,21,34,55,89,144·····这个数列为“斐波那契数列”,这些数被称为“斐波那契数”。
经计算发现相邻两个斐波那契数的比值是随序号的增加而逐渐逼近黄金分割比。由于斐波那契数都是整数,两个整数相除之商是有理数,而黄金分割是无理数,所以只是不断逼近黄金分割。[6]
发展简史
所谓黄金三角形是一个等腰三角形,其底与腰的长度比为黄金比值,正是因为其腰与边的比为(√5-1)/2而被称为黄金三角形。黄金分割三角形是唯一一种可以用5个而不是4个与其本身全等的三角形来生成与其本身相似的三角形的三角形。由五角形的顶角是36度可得出黄金分割的数值为2sin18度(即2*sin(π/10))。
将一个正五边形的所有对角线连接起来,在五角星中可以找到的所有线段之间的长度关系都是符合黄金分割比的,所产生的五角星里面的所有三角形都是黄金分割三角形。[7]
应用实例
 毕达哥拉斯公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,关于黄金分割比例的起源大多认为来自毕达哥拉斯学派。1:0.618就是黄金分割。这是一个伟大的发现。
毕达哥拉斯公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,关于黄金分割比例的起源大多认为来自毕达哥拉斯学派。1:0.618就是黄金分割。这是一个伟大的发现。
公元前4世纪,古希腊数学家欧多克索斯第一个系统研究了这一问题,并建立起比例理论。他认为所谓黄金分割,指的是把长为L的线段分为两部分,使其中一部分对于全部之比,等于另一部分对于该部分之比。而计算黄金分割最简单的方法,是计算斐波那契数列1,1,2,3,5,8,13,21,...第二位起相邻两数之比,即2/3,3/5,5/8,8/13,13/21,...的近似值。[3]
公元前300年前后欧几里得撰写《几何原本》时吸收了欧多克索斯的研究成果,进一步系统论述了黄金分割,成为最早的有关黄金分割的论著。
黄金分割在文艺复兴前后,经过阿拉伯人传入欧洲,受到了欧洲人的欢迎,他们称之为"金法",17世纪欧洲的一位数学家,甚至称它为"各种算法中最可宝贵的算法"。这种算法在印度称之为"三率法"或"三数法则",也就是我们常说的比例方法。
中世纪后,黄金分割被披上神秘的外衣,意大利数学家帕乔利将中末比为神圣比例,并专门为此著书立说。德国天文学家开普勒称黄金分割为神圣分割。[3][8]
词条图册
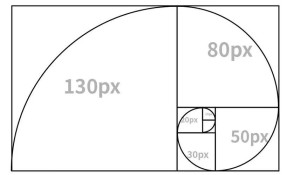 黄金分割黄金分割具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值,这一比值能够引起人们的美感,被认为是建筑和艺术中最理想的比例。[5]
黄金分割黄金分割具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值,这一比值能够引起人们的美感,被认为是建筑和艺术中最理想的比例。[5]
画家们发现,按0.618:1来设计的比例,画出的画最优美,在达·芬奇的作品《维特鲁威人》、《蒙娜丽莎》、还有《最后的晚餐》中都运用了黄金分割。而现今的女性,腰身以下的长度平均只占身高的0.58,因此古希腊的著名雕像断臂维纳斯及太阳神阿波罗都通过故意延长双腿,使之与身高的比值为0.618。建筑师们对数字0.618特别偏爱,无论是古埃及的金字塔,还是巴黎的圣母院,或者是近世纪的法国埃菲尔铁塔,希腊雅典的巴特农神庙,都有黄金分割的足迹。[5]

-
呼和浩特探岳现金优惠3.5万 成都丰田锐志最高优惠2.2万
2025-09-28 11:44:21 查看详情 -
西安大众速腾现金优惠2.3万 成都沃尔沃XC90优惠三万元
2025-09-28 11:44:21 查看详情 -
西安大众速腾现金优惠2.3万 驾驭快感
2025-09-28 11:44:21 查看详情 -
呼和浩特探岳现金优惠3.5万 再送装潢礼包
2025-09-28 11:44:21 查看详情 -
重庆林肯Z现金优惠1.2万元 成都丰田锐志购车优惠2.4万元
2025-09-28 11:44:21 查看详情 -
成都丰田亚洲狮现金优惠3万元 成都丰田锐志购车优惠2.4万元
2025-09-28 11:44:21 查看详情 -
珠海大众宝来现金优惠2.7万 外观流畅
2025-09-28 11:44:21 查看详情 -
成都标致307两厢优惠5千元 长沙现代悦动现金优惠1.2万
2025-09-28 11:44:21 查看详情 -
大连沃尔沃S90现金优惠7.2万 购S80送全购置税加全险
2025-09-28 11:44:21 查看详情 -
长城金刚炮AT车型将于3月2日上市 6.89万
2025-09-28 11:44:21 查看详情


 求购
求购

