- 自然对流换热

自然对流换热
简介
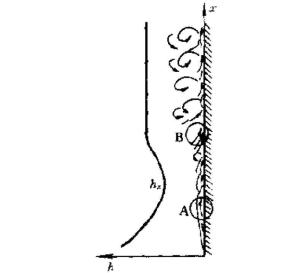 图1自然对流亦有层流和湍流之分。以贴近一块热竖壁的自然对流为例来作分析,其自下而上的流动景象如图1所示。
图1自然对流亦有层流和湍流之分。以贴近一块热竖壁的自然对流为例来作分析,其自下而上的流动景象如图1所示。
在壁的下部,流动刚开始形成,它是有规则的层流;若壁面足够高,则上部流动会转变为湍流。
不同的流动状态对换热具有决定性影响。
层流时,换热热阻完全取决于薄层的厚度。从换热壁面下端开始,随着高度的增加,层流薄层的厚度也逐渐增加。与此相对应,局部表面传热系数也随高度增加而减小。如果壁面足够高,流体的流动将逐渐转变为湍流。湍流时换热规律有所变化。研究表明,旺盛湍流时的局部表面传热系数几乎是个常量。[1]
分类
自然对流换热分为大空间自然对流换热和有限空间自然对流换热两类。流体在大空间作自然对流时,流体的冷却过程与加热过程互不影响。这类问题比较简单,但总结出的关联式却具有很大的实用意义,它可以应用到比形式上的大空间更广的范围。因为在许多实际问题中,虽然空间不大,但热边界层并不相互于扰,因而可以应用大空间自然对流换热的规律计算。换句话说,就是可以把它当作大空间问题来处理。
所谓大空间,实际上只要边界层不受干扰就可以适用,不必拘泥于几何形式上的很大或无限大。[2]
影响因素
由于流体内部温度差引起密度不同而形成浮升力,在此浮升力引发的运动下所产生的换热过程,又称自由运动换热。热力管道、热力设备、锅炉炉体等与周围空气之间的换热都是自然对流换热。它的强度取决于流体沿固体换热表面的流动状态及其发展情况,而这些又与流体流动的空间和换热表面的形状、尺寸、表面与流体之间的温差、流体的种类与物性参数等许多因素有关,是一个受众多因素影响的复杂过程。
求解方法
近年来已经提出了许多数值计算方法 ,用来求解流体流动及对流换热问题。常用的方法有:有限差分法、有限元法、边界元法、有限分析法。
从方法发展与积累的经验、实施的难易及应用的广泛性等方面 ,就目前而言 ,随着计算机的应用 ,有限差分法还是一种通用的方法。有限差分法可以采用不同的差分格式 ,通常选用显格式和隐格式。凯勒单元法实质上也是一种隐格式 ,其主要特点有:无条件稳定 ,可用变步长网格、二阶精度 ,可取较大的步长值、联立方程求解的程序编制简便 ,但在建立离散方程系数时 ,其运算比较复杂。由于凯勒单元法有其固有特性 ,因此 ,早在 70年代 ,就有许多的研究者将此法用于求解边界层问题。在最近20年中 ,此方法发展已比较成熟。

-
浙江省自然科学基金委员会
2025-10-31 17:13:10 查看详情 -
南京林业大学学报:自然科学版
2025-10-31 17:13:10 查看详情 -
石家庄铁道大学学报(自然科学版)
2025-10-31 17:13:10 查看详情 -
习水中亚热带常绿阔叶林国家级自然保护区
2025-10-31 17:13:10 查看详情 -
云南师范大学学报(自然科学版)
2025-10-31 17:13:10 查看详情 -
青铜峡水库湿地自然保护区
2025-10-31 17:13:10 查看详情 -
一个自然科学家在贝格尔舰上的环球旅行记
2025-10-31 17:13:10 查看详情


 求购
求购










