- 相交线

相交线
定义
在同一平面内,两条直线的位置关系:相交、平行。
有唯一公共点的两条直线叫作相交线。
邻补角和对顶角
如图1所示,直线相交,形成4个角。
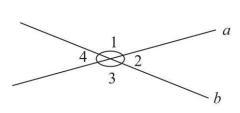 图1
图1
(1)邻补角:∠1和∠2有一条公共边.它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角。如:∠1和∠4,∠2和∠3等。
(2)对顶角:∠1和∠3有一个公共顶点,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角。如:∠2和∠4。
对顶角的性质:对顶角相等
关键提醒:①邻补角是有特殊位置关系的两个互补的角,要注意区别补角与邻补角这两个概念,互为补角的两个角只强调数量关系,不强调位置关系;邻补角不仅强调数量关系,同时也强调位置关系。
②对顶角和邻补角是成对出现的,只有当两条直线相交时,才产生对项角和邻补角。
垂线
(1)垂直:两条直线相交所成的四个角中,有一个角为90°时,称这两条直线互相垂直。
(2)垂线:两条直线互相垂直,其中的一条直线叫作另一条直线的垂线,交点叫作垂足。
(3)性质:①过一点有且只有一条直线与已知直线垂直;②连接直线外一点与直线上各点的所有线段中,垂线段最短,简单说成:垂线段最短。
关键提醒:①对于垂线的性质,必须强调“在同一平面内”,否则,在空间里,经过一点与已知直线垂直的直线有无数条;②“过一点”包括直线上一点和直线外一点,“有”表示存在,“只有”表示唯一。
(4)点到直线的距离:直线外一点到这条直线的垂线段的长度,叫作点到直线的距离。
关键提醒:垂线是直线,垂线段特指一条线段,点到直线的距离是指垂线段的长度,是一个数量,是有单位的。[1]
例题如图2所示,直线AB,CD相交于点0,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )。
A.35° B.45° C.55° D.65°
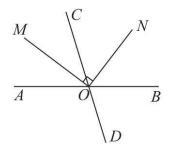 图2
图2
解析:因为射线OM平分∠AOC,∠AOM=35°,所以∠MOC=35°,因为ON⊥OM,所以∠MON=90°,所以∠CON=∠MON-∠MOC=90°-35°=55°。
答案:C
各角信息
三者位置特点、图形特征见表1。
| 角的名称 | 位置特点 | 图形特征 |
| 同位角 | 在两条被截直线的同旁,在截线同侧 | 形如字母“F”,如图3 |
| 内错角 | 在两条被截直线的内部,在截线两侧 | 形如字母“Z”,如图4 |
| 同旁内角 | 在两条被截直线的内部,在截线同侧 | 形如字母“n”,如图5 |
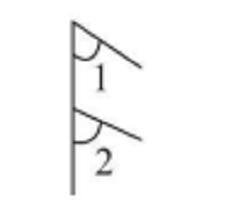 图3
图3
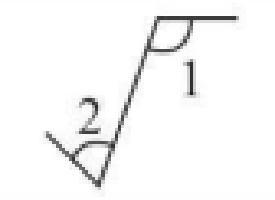 图4
图4
 图5
图5
词条图册
| 角的名称 | 位置特点 | 图形特征 |
| 同位角 | 在两条被截直线的同旁,在截线同侧 | 形如字母“F”,如图3 |
| 内错角 | 在两条被截直线的内部,在截线两侧 | 形如字母“Z”,如图4 |
| 同旁内角 | 在两条被截直线的内部,在截线同侧 | 形如字母“n”,如图5 |

-
Chamberlain线
2025-09-16 04:59:38 查看详情 -
关于奥迪PA生产线是什么意思介绍(奥迪PA生产线是什么意思)
2025-09-16 04:59:38 查看详情


 求购
求购









