- 椭圆型偏微分方程

椭圆型偏微分方程
定义
椭圆型偏微分方程是偏微分方程的一个类型,简称椭圆型方程。这类方程主要用来描述物理只能的平衡稳定状态,如定常状态下的电磁场、引力场和反应扩散现象等。
椭圆型方程是由方程中主部的系数来界定的。对两个自变量的二阶线性或半线性方程
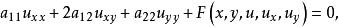 在不等式
在不等式 成立的区域内,就称方程是椭圆型的。
成立的区域内,就称方程是椭圆型的。
此时,可以通过自变量的非奇异变换将方程化为标准型
 对于高阶线性方程,设
对于高阶线性方程,设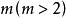 阶线性偏微分算子为
阶线性偏微分算子为
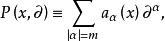 其中,
其中,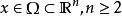 。该偏微分算子的主部是
。该偏微分算子的主部是
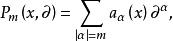 若对
若对![]() 及任意非零向量
及任意非零向量![]() 都有
都有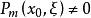 ,则称方程
,则称方程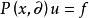 在点
在点![]() 是椭圆型的。如果
是椭圆型的。如果![]() 中是线性椭圆型方程。
中是线性椭圆型方程。
种类
线性
线性椭圆型方程的典型代表是拉普拉斯方程(也叫调和方程)
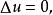 其中,
其中,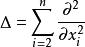 ,这个算子叫拉普拉斯算子(Laplace operator),也叫调和算子。
,这个算子叫拉普拉斯算子(Laplace operator),也叫调和算子。
可以说,调和方程是最基本,同时也是最重要的线性椭圆型方程。
非线性
对于非线性方程,也可以定义椭圆型方程。
例如,考虑二阶实系数拟线性方程
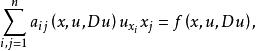 其中,
其中,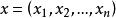 。如果对任意非零向量
。如果对任意非零向量![]() ,
,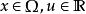 及
及![]() ,有
,有
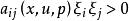 就称方程是
就称方程是![]() 中的拟线性椭圆型方程。类似地,可以定义高阶拟线性椭圆型方程。[1]
中的拟线性椭圆型方程。类似地,可以定义高阶拟线性椭圆型方程。[1]

相关百科
-
非线性方程组数值解法
2025-10-31 06:35:00 查看详情 -
F1方程赛车逆向设计
2025-10-31 06:35:00 查看详情 -
三款小排量小型SUV雪铁龙C3 1.8L车型的油耗方程式
2025-10-31 06:35:00 查看详情 -
成都车展:一汽奔腾无限方程架构发布/第三代B70将问世 e
2025-10-31 06:35:00 查看详情 -
雪铁龙C3 1.8L车型的油耗方程式
2025-10-31 06:35:00 查看详情 -
东风雪铁龙凡尔赛C5 1.8L车型的油耗方程式
2025-10-31 06:35:00 查看详情 -
雪铁龙天逸对比大众途岳 1.8L车型的油耗方程式
2025-10-31 06:35:00 查看详情


 求购
求购



