- 范德瓦尔斯方程

范德瓦尔斯方程
范德瓦尔斯方程
![]()
式中
p 为气体的压强
a 为度量分子间引力的参数
b 为每个分子平均占有的空间大小(即气体的体积除以总分子数量)
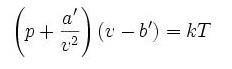 范德瓦尔斯方程
范德瓦尔斯方程
T 为热力学温度
R 为普适气体常数
m 为气体质量
M 为摩尔质量
在第二个方程里,气体物质的量为 1mol
v 为体积
k 为玻尔兹曼常数
范德瓦尔斯常量
下表列出了部分气体的a,b 的值[1]
| 气体 | a / (atm·L^2/mol^2) | b / (L/mol) |
| 氢 | 0.191 | 0.0218 |
| 氧 | 1.360 | 0.03183 |
| 氮 | 1.390 | 0.03913 |
| 氯 | 6.493 | 0.05622 |
| 氦 |
0.03412 | 0.02370 |
| 氖 |
0.2107 | 0.01709 |
| 汞蒸气 | 8.093 | 0.01696 |
| 二氧化碳 | 3.592 | 0.04267 |
| 水蒸气 | 5.464 | 0.03049 |
适用范围
| 气体 | a / (atm·L^2/mol^2) | b / (L/mol) |
| 氢 | 0.191 | 0.0218 |
| 氧 | 1.360 | 0.03183 |
| 氮 | 1.390 | 0.03913 |
| 氯 | 6.493 | 0.05622 |
| 氦 |
0.03412 | 0.02370 |
| 氖 |
0.2107 | 0.01709 |
| 汞蒸气 | 8.093 | 0.01696 |
| 二氧化碳 | 3.592 | 0.04267 |
| 水蒸气 | 5.464 | 0.03049 |
方程提出
范氏方程对气-液临界温度以上流体性质的描写优于理想气体方程。对温度稍低于临界温度的液体和低压气体也有较合理的描述。
但是,当描述对象处于状态参量空间(P,V,T)中气液相变区(即正在发生气液转变)时,对于固定的温度,气相的压强恒为所在温度下的饱和蒸气压,即不再随体积V(严格地说应该是单位质量气体占用的体积,即比容)变化而变化,所以这种情况下范氏方程不再适用。
词条图册
水分子之间的范氏引力(中国大陆的中学教科书称为“范德瓦尔斯力”或“范德华力”)
一个双原子分子的排斥体积(图中黑色的部分)下面以理想气体状态方程为基础,推导范氏方程。若把气体视为由体积无限小、相互之间无作用力的分子组成,这种模型便是理想气体模型,与其相对应的状态方程是:
若抛弃前一个的假设,把组成气体的分子视为有一定大小的刚性球(其半径称为范德瓦尔斯半径),用b 表示这些“球”的体积,上面的方程便改写为:
在这里,每个分子的“占有体积”v 被所谓“排斥体积”v - b 代替,反映了分子在空间中不能重叠。若气体被压缩至体积接近分子体积之和(即分子间空隙v - b 趋向于0),那么其压强将趋于无穷大。
下一步,我们考虑原子对之间的引力。引力的存在会使分子的平均亥姆霍兹自由能下降,减少量正比于流体的密度。但压强的大小满足热力学关系
式中A* 为每个分子的亥姆霍兹自由能。由此得到,引力使压强减小的量正比于1/v²。记该比例常数为a,可得
这便是范氏方程。

-
奇驭计划专属福利,瓦尔塔汽车蓄电池618钜惠 别再犹豫了
2025-09-21 17:58:38 查看详情 -
迈尔斯布里格斯类型指标
2025-09-21 17:58:38 查看详情 -
非线性方程组数值解法
2025-09-21 17:58:38 查看详情 -
斯科特·查尔斯·斯图瓦特
2025-09-21 17:58:38 查看详情


 求购
求购








