闭包算子

形成拓扑空间子集的闭包有这些性质，如果所有子集的集合按包含 ⊆ 来排序。(注意拓扑闭包算子不由这些性质来刻画；完全特征刻画请参见库拉托夫斯基闭包公理。)

另一个典型闭包算子是: 选取群G和任何G的子集X，设C(X) 是X生成的子群，就是说包含X的G的最小子群。则C是在G的子集的集合上闭包算子，它按包含 ⊆ 排序。类似的例子有向量空间的给定子集所生成的子空间，域的给定子集生成的子域，甚至泛代数意义上任何代数的给定子集生成的子代数。

从实数到实数的上取整函数，它对所有实数x指派不小于x的最小整数，也是闭包算子。

给定闭包算子C，P的“闭合元素”是一个元素x，它是C的不动点，或者等价的说，它在C的像中。如果a是闭合的并且x是任意的，则有着x≤a当且仅当C(x) ≤a。所以C(x) 是大于或等于x的最小闭合元素。我们看到C被唯一的确定自闭合元素的集合。

所有伽罗瓦连接都引发一个闭包算子(其条目中有解释)。事实上，所有闭包算子都以这种方式引发自伽罗瓦连接。伽罗瓦连接不唯一的确定自闭包算子。引发闭包算子C的伽罗瓦连接可以描述如下: 如果A是关于C的闭合元素的集合，则C:P→A是在P和A之间的伽罗瓦连接的下伴随，带有上伴随为把A嵌入到P中。进一步的说，所有把某个子集嵌入P的下伴随都是闭包算子。“闭包算子是嵌入的下伴随”。但是注意不是所有嵌入都有下伴随。

任何偏序集合P都可以被看作范畴，带有从x到y的一个单一态射当且仅当x≤y。在偏序集合P上的闭包算子就是在范畴P上的monad。等价的说，闭包算子可以被单做有额外的幂等和扩展性质的 Posets 范畴的 endofunctor。

如果P是完全格，则P的子集A是对某个P上闭包算子的闭合元素的集合，当且仅当A是在P上的Moore家族，就是说P的最大元素在A中，并且任何A中非空子集的下确界(交运算)也在A中。任何这样的集合A自身是带有继承自P的次序的完全格(但是上确界(并运算)可能不同于P的)。在P上的闭包算子自身形成一个完全格；在闭包算子上的次序定义为C1≤C2当且仅当C1(x) ≤C2(x) 对于所有P中的x。

闭包算子有很多应用。

在拓扑结构中，闭包算子是拓扑关闭算子，必须满足：

对于所有的(注意当n=0时)。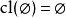

在代数和逻辑上，许多闭包算子是有限的，即他们满足：

在通用逻辑中，闭包算子也被称为结果算子。

在理论计算机科学中重要的部分有序集理论中，闭包算子有另外的定义。

如上面提及的，闭包可以被看作来自伽罗瓦连接。如果把伽罗瓦连接推广为伴随函子，闭包的对应是monad。