- 非结合代数
非结合代数
定义
从结合代数的定义中把乘法适合结合律这一条件删去,就是非结合代数的定义。李代数、若尔当代数、交错代数,以及李型代数、若尔当型代数都是非结合代数最重要的类型。非交换若尔当代数、右交错代数、交错李代数、马尔采夫代数、幂结合代数则是李代数、交错代数或若尔当代数的推广。非结合代数中的乘法往往满足某些恒等式。
环论
环论是研究环的性质及其运算 规律的代数分支学科。近代环论也 包含了非结合代数。“环”是抽象代 数研究中的基本对象之一。
环和理想的构造在19世纪已为 人熟知,并应用在戴德金(Dedekind,R.)和克劳尼克(Kronecker, L.)等关于代数数的著作中。克劳 尼克(Kronecker,L.)将环称为“order”,希尔伯特(Hilbert,D.)才引 进了“ring (环)”这一词。但是抽 象的理论是在20世纪发展起来 的。至诺德爱米(Noether,N.)将其 置于系统化和公理化的基础上。
环论和群的概念有密切关系, 设S是一个集合,它在加法之下 构成Abel群,在乘法运算之下是 半群,对加法满足分配律,即对:
∀a, b, c∈S
a(b+c)=ab+ac
(a+b)c=ac+bc
在环中,对乘法而言:ab=0⇏a=0或b=0如果有a∈S, 存在b∈S,使ab=0 (ba=0),则 说a是S中的一个左 (右) 零因 子。不含零因子的交换环称为整 环。数域上的多项式环也是整环。 n阶矩阵环则不是整环。
正如不变子群在群的研究中所 起作用一样,理想的概念对环的研 究至关重要。对环S中的非空子集 A,如果A关于S中的两种运算构 成环,则A是S的子环。进一步, 对S中的子环A, 如果∀m∈S, a∈ A,有xa,ax∈A,则A称为环S 的一个理想。显然S中理想的交集 仍是S的理想,当A是环S的一个 理想时,由加法运算作出商群 S/A,此商群对乘法而言,易证其 为半群,从而S/A构成环,称为 商环,或称S关于A的剩余类环。
环的同态和同构是研究环的重 要工具。
设f是环A到环Ā的一个映 照, 如果对∀a·b∈A有f(a+b) =f(a)+f(b),f(ab)=f(a)f(b),则说f 是A到Ā的同态映照, 当f是满射 时, 则说f是A到Ā的满同态; 而 如果f是双射, 则称f是A和Ā的 同构映照, 并说A和Ā同构,记 为A≃Ā。
设f是A到A的同态映照,o 是中零元素 (加群的单位元) 记 kerf={x∈A|f(x)=0}称为同态映 照f之核,kerf关于加法构成群, 关于乘法构成半群。 又∀x∈A, y ∈kerf,
f(xy)=f(x) f(y)=0
f(yx)=f(y) f(x)=0
∴xy,yx∈kerf,故kerf为A 的一个理想。由此可得环的同态基 本定理。
A是环,则A的任一商环都 是A的同态象, 反之, 如果Ā是 A在f之下的同态象,则有
A≃A/kerf
由环的概念,可引伸出代数的 概念,设S是一个环,如果作为 加法群,它是域K上的向量空 间,域K上的数乘和S上的乘法 可交换,即α∈K,a·b∈S,则 (αa)b=α(ab),则S称为一个 代数,进一步可讨论代数的表示理 论。
环论在域论中起决定性作 用,在泛函分析中也获得广泛应用。
类型
李代数
李代数是一种非结合代数,其乘法满足恒等式:x2=0和(xy)z+(yz)x+(zx)y=0。在一个域F(特征非2)上结合代数〈A,+,·〉中,将原来的有结合律的乘法·换成新引入的乘法×: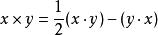
得到的〈A,+,×〉就是一个李代数。由结合代数A如此得来的李代数,记作A_。
若尔当代数
若尔当代数是20世纪30年代P.若尔当、J.冯·诺伊曼和E.威格纳等人,在研究量子力学的基础时引用的一种非结合代数。在描述量子力学基础时涉及结合代数〈A,+,·〉(希尔伯特空间的算子代数)中,将原来的有结合律的乘法·换成新的乘法:
就得到非结合代数〈A,+,。〉,其中乘法。满足恒等式x。y=y。x和x2。(y。x)=(x2。y)。x,这里x2=x。x;后来,就把满足这两个恒等式的代数称为若尔当代数, 并将如此得出的若尔当代数记作 A+。之所以规定乘法。 如(2),是因为考虑到:若x、y都是埃尔米特算子,则x。y也是埃尔米特算子,但一般说来,x·y已不是埃尔米特算子。
李型代数和若尔当型代数的概念,早在20世纪40年代末期就由A.A.阿尔贝特提出来了,但它的重要性还是自70年代以来由于理论物理的需要,例如在统计物理、力学、原子物理中讨论无势相互作用等,才显示出来。所谓一个代数〈A,+,·〉为李型代数,是指〈A,+,×〉是李代数,其中新乘法×由(1)定义。结合代数和李代数都是李型代数。所谓一个代数〈A,+,·〉为若尔当型代数,是指〈A,+,。〉是若尔当代数,其中新乘法。由(2)定义。结合代数和交错代数都是若尔当型代数。[2]
交错代数
交错代数的产生是由于推广数系。令Q表实数域R上四元代数。它是可除结合代数,取其标准基1,i,j,k,则Q中元素 α有惟一的表示式: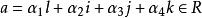
再定义α的共轭元为: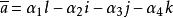
则α→是Q的一个对合,且有α=α∈R,α+∈R。所谓Q的一个对合,是指Q 的反自同构,且其平方等于恒等自同构。
![]() 、
、![]() 、
、![]() 式子仿照由复数作四元数的方法,用四元数来构造八元数即凯莱数。令C是一切四元数对(α,b)的集合,规定式子
式子仿照由复数作四元数的方法,用四元数来构造八元数即凯莱数。令C是一切四元数对(α,b)的集合,规定式子![]() ,其运算:(α,b)+(с,d)=(α+с,b+d);α(α,b)=(αα,αb);(α,b)·(с,d)=(αс-b,dα=b),这里α,b,с,d∈Q,、分别是с、d的共轭元,α∈R。由直接验证可知,C 是实数域R上的8维代数,有单位元(1,0)。它是可除代数,即对于任意u,v∈C,u≠0,在C 中ux=v和xu=v有解。它的乘法不适合结合律,却满足恒等式x2y=x(xy)和yx2=(yx)x 。把满足这两个恒等式的代数称为交错代数。凯莱代数是交错可除代数的一个例子。结合代数是交错代数。刻画交错代数与结合代数的接近程度的是阿廷定理:一个代数A是交错代数,当且仅当其中任意两个元素生成的子代数是结合代数。
,其运算:(α,b)+(с,d)=(α+с,b+d);α(α,b)=(αα,αb);(α,b)·(с,d)=(αс-b,dα=b),这里α,b,с,d∈Q,、分别是с、d的共轭元,α∈R。由直接验证可知,C 是实数域R上的8维代数,有单位元(1,0)。它是可除代数,即对于任意u,v∈C,u≠0,在C 中ux=v和xu=v有解。它的乘法不适合结合律,却满足恒等式x2y=x(xy)和yx2=(yx)x 。把满足这两个恒等式的代数称为交错代数。凯莱代数是交错可除代数的一个例子。结合代数是交错代数。刻画交错代数与结合代数的接近程度的是阿廷定理:一个代数A是交错代数,当且仅当其中任意两个元素生成的子代数是结合代数。
幂结合代数
所谓幂结合代数,是指一代数中任意元素生成的子代数都是结合代数。可以证明,以上提到的各种类型代数都是幂结合代数。
在非结合代数中进行计算时,某些恒等式具有很重要的作用。在交错代数中有常用的毛凡恒等式:x(yzy)=[(xy)z]y,(yzy)x=y[z(yx)],(xy)(zx)=x(yz)x;在若尔当代数中有常用的恒等式: {xyx}2={x{yx2y}x},zU(xU(y))=zU)U(x)U(y),其中{xyx}=(xy)z+(yz)x-(xz)y,而算子: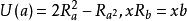 。
。
这里的第二个恒等式,常称为麦克唐纳恒等式。[3]
理论发展
非结合代数理论在很大程度上是沿着结合环与结合代数的发展道路发展的。结合环与结合代数的发展初期,大致可分为三个阶段:有限维代数的韦德伯恩理论,对右理想适合极小条件的环的阿廷理论,以雅各布森根和本原环理论为中心的一般环理论。目前,各种非结合代数都有着不同的发展深度,有些还处于一种相当于结合代数的韦德波恩理论的阶段,例如马尔采夫代数,而交错代数和若尔当代数的发展最快,大致完成了上述结合环的三个阶段。以下是关于交错代数和若尔当代数的一些结果的简介。
推广的弗罗贝尼乌斯定理:实数域上有限维交错可除代数只有实数域、复数域、四元数代数以及凯莱代数等四种。它们在实数域上的维数是 1,2,4,8。与此定理有关的一个有趣问题是:在实数域中,n个平方数的和乘以n个平方数的和,仍是n个平方数的和吗?利用这个定理中的四种代数以及其中的共轭元素概念,不难作出当n=1,2,4,8时确是成立的结论。A. 胡尔维茨以及阿尔贝特指出,n只能是1,2,4,8,从而完满地解决了这个问题。
R.博特、J.W.米尔诺和M.克拉尔应用代数拓扑工具,证明了一个重要的定理:实数域上有限维(非结合)可除代数的维数,只能是1,2,4,8。
阿尔贝特、R.D.谢弗、A.J.佩尼罗和M.佐恩等人证明了与有限维结合代数的韦德伯恩定理相平行的关于交错代数和若尔当代数的定理。
单代数的分类是有限维代数研究中的一个重要问题。设A是域F上有限维单代数,而且是交错代数或若尔当代数,此时A必有单位元1,定义C={с|с∈A,сx=xс,с,x,y之间的乘法适合结合律,凬x,y∈A}是A的中心。可以证明,C必是一个域。如果C=F,那么A称为F上中心单代数。交错单代数的品种不多,域F上有限维中心单代数,或是结合代数,或是F上凯莱-迪克森代数。任意域F上的凯莱-迪克森代数是F上8维代数,其定义与实数域上凯莱代数的定义类似,它是实数域上凯莱代数的推广,其中也有共轭元素的概念。E.克莱因菲尔德把上述结果推广到任意交错环上。
中心单若尔当代数的类型则较多,有A、B、C、D、K型。仅仅就例外单若尔当代数(K型单代数)而论,它和五个例外单李代数类型处于类似的地位。取D为域F上的一个凯莱-迪克森代数,D3表D上三阶矩阵组成的代数,任取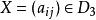 ,令
,令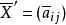 ,即将矩阵X转置,并把每一系数换成其共轭元素。可知映射:
,即将矩阵X转置,并把每一系数换成其共轭元素。可知映射: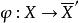 是F上代数D3的一个对合。令
是F上代数D3的一个对合。令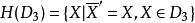 ,即H(D3)是D3中关于对合的所有埃尔米特元素的全体。可以证明,H(D3)关于若尔当乘法
,即H(D3)是D3中关于对合的所有埃尔米特元素的全体。可以证明,H(D3)关于若尔当乘法 作成一个若尔当代数。注意到D是F上 8维交错代数,还可以证明<H(D3),+,。>是F上中心单代数,其维数是27,并且是例外若尔当代数。例外单李代数与凯莱-迪克森代数也有密切关系。所谓例外的若尔当代数,即指不是特殊的若尔当代数。若A是结合代数,则A_是李代数,A+是若尔当代数。A_(A+)、A_(A+)的子代数以及与之同构者,称为特殊李代数(特殊若尔当代数)。虽然不是每一个李环都是特殊的,但是著名的伯克霍夫-维特定理指出,域上李代数都是特殊的。Α.И.希尔绍夫的定理又指出,任意具有两个生成元的若尔当代数(环)是特殊的。
作成一个若尔当代数。注意到D是F上 8维交错代数,还可以证明<H(D3),+,。>是F上中心单代数,其维数是27,并且是例外若尔当代数。例外单李代数与凯莱-迪克森代数也有密切关系。所谓例外的若尔当代数,即指不是特殊的若尔当代数。若A是结合代数,则A_是李代数,A+是若尔当代数。A_(A+)、A_(A+)的子代数以及与之同构者,称为特殊李代数(特殊若尔当代数)。虽然不是每一个李环都是特殊的,但是著名的伯克霍夫-维特定理指出,域上李代数都是特殊的。Α.И.希尔绍夫的定理又指出,任意具有两个生成元的若尔当代数(环)是特殊的。
K.A.日弗拉科夫完整地刻画了阿廷交错环。由于缺乏适当的“单侧理想”概念,长期未能定出与阿廷结合环相平行的阿廷-若尔当环的概念。 D.M.托平引入二次理想概念:如果对若尔当环 A的子环 B的任意元素 b有AU(b)吇B,那么B 称为二次理想。N.雅各布森刻画了对二次理想有极小条件的若尔当环,与结合环中的阿廷理论相平行。利用算子U可定义二次若尔当代数,K.麦克里芒作了许多贡献。结合环的雅各布森根和莱维茨基根等在若尔当环和交错环中,都有相应的讨论。对交错代数和若尔当代数都有表示论的研究。交错环与若尔当环和投射平面有联系。若尔当代数不仅与李代数、代数群有着联系,而且对实分析和复分析都有应用。[4]

-
资产负债表日后非调整事项
2025-09-20 18:31:37 查看详情 -
英菲尼迪越野车报价 英非尼迪是什么车系?
2025-09-20 18:31:37 查看详情 -
98年的营转非的富康两厢汽车大修一下发动机需要多少钱?
2025-09-20 18:31:37 查看详情 -
营转非汽车价格怎么样 营转非的车能买吗?
2025-09-20 18:31:37 查看详情 -
英菲尼迪g25论坛 英非尼迪G25的隔音效果怎么样
2025-09-20 18:31:37 查看详情


 求购
求购




