- 闪耀光栅

闪耀光栅
简介
闪耀光栅(blazed grating)
当 光栅刻划成锯齿形的线槽断面时,光栅的 光能量便集中在预定的方向上,即 某一 光谱级上。从这个方向探测时, 光谱的强度最大,这种现象称为 闪耀(blaze),这种光栅称为闪耀光栅。
在这样刻成的闪耀光栅中,起 衍射作用的槽面是个光滑的平面,它与光栅的表面一 夹角,称为 闪耀角(blaze angle)。最大 光强度所对应的 波长,称为 闪耀波长(blaze wavelength)。
通过闪耀角的设计,可以使光栅适用于某一特定 波段的某一级光谱。
优点
透射光栅有很大的缺点,主要是衍射图样中没有色散的零级主最大总是占总光能的很大一部分,其余光能分散在各级光谱中,而实际使用光栅时往往只利用它的某一级。这对光栅的应用是很不利的。
闪耀光栅则实现了 单缝衍射中央最大值的位置从没有色散的零级光谱转移到其他有色散的光谱级上。
CD光盘可以看作粗制的闪耀光栅。
 闪耀光栅
闪耀光栅
光栅教程
衍射光栅教程
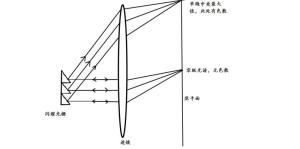 无论是透射式还是反射式的衍射光栅,都能通过光栅上的周期性结构将不同波长的光分开。该结构会影响入射波的幅值/相位/幅值与相位,引起出射波的干涉。对透射光栅,周期性的结构可看作许多紧密排列的狭缝。通过将光照度分别作为波长的函数和多缝位置的函数进行联立求解,我们得到下式,它可以应用在一切衍射光栅上:
无论是透射式还是反射式的衍射光栅,都能通过光栅上的周期性结构将不同波长的光分开。该结构会影响入射波的幅值/相位/幅值与相位,引起出射波的干涉。对透射光栅,周期性的结构可看作许多紧密排列的狭缝。通过将光照度分别作为波长的函数和多缝位置的函数进行联立求解,我们得到下式,它可以应用在一切衍射光栅上:
(1) 透射光栅
透射光栅是一种获得普遍使用的光栅。这种光栅是在透明基底上刻划或腐蚀出一个周期性的平行结构得到的。这种结构可以使光在空间上分散开。透射光栅样品如图1所示。
图1所示的衍射光栅是由一组周期性的、间距为的狭槽构成的。入射光以相对于光栅表面法线的入射角入射,级出射光相对光栅表面法线的出射角为。通过一些几何变换,并利用透射式衍射光栅的通用公式(公式1),可以得到透射式衍射光栅的公式:
(2)
闪耀光栅,也被称为小阶梯光栅,是设计的一种在特定衍射级别产生最大衍射效率的特定的反射或者投射衍射光栅结构。这意味着,在设计的衍射级别上光功率占大多数,同时在其他级别(尤其是零级)光功率的损失最小。 基于这种设计,一个闪耀光栅对应一个特定的波长使用,称为闪耀波长。
闪耀波长是闪耀光栅的三个基本特点之一,其余两个如图3所示为,槽间距(或工作面间距)和闪耀角。.闪耀角是光栅反射面(工作面)与光栅表面之间的夹角,也是反射面法线与光栅平面法线之间的夹角。
以上讨论的闪耀光栅的几何性质与透射光栅和反射光栅相同;入射角和出射角都是相对光栅表面法线确定。但是,显著的不同是表面反射图样由闪耀角决定,而不是由光栅表面法线确定。这使得只需改变光栅闪耀角就能改变衍射图样。
闪耀光栅的零级反射如图4所示。当= 0时,入射角为的光反射后反射角为。根据公式2,唯一解为=。 这与平整表面上的镜面反射类似。
Figure 5.闪耀光栅的镜面反射
衍射光栅上的镜面反射与普通平面上的不同,它与光栅表面形状有关,如图5所示。闪耀光栅上发生镜面反射时,反射角与闪耀角大小有关。进行一些简单的几何变换,我们可以发现
(3)
利用公式2、公式3,我们可以发现闪耀光栅的关于其2倍的闪耀角的一个等式:
(4)
有一种情况在单色仪和光谱仪中具有重要作用,这就是Littrow结构。在这种结构中,射入光的入射角与衍射角是相同的,即=,且> 0, 于是可以得到
(5)
Littrow结构角,与最强级次(= 1)、设计波长和光栅槽间距有关。容易证明,在设计波长下,Littrow结构入射角与闪耀角相等。Thorlabs所有闪耀光栅的Littrow角/闪耀角都可以在光栅规格说明书表格中找到。
容易观察到,在正入射情况下,与波长相关的角间距随着衍射级次的增高而增大。(当=0时,随着的增高而增大)。相对于较低级次,使用较高级次的衍射图样有两个主要缺点: (1) 级次越高,效率越低; (2)级次越高,自由光谱区间越小。自由光谱区间定义如下:
(6)
其中是中心波长,是级次。
上面第一个关于较高级次衍射图样能量低的问题可以利用 阶梯光栅解决,这是一种特殊的刻划光栅,有着极大的衍射角。高衍射角很适于将能量集中到较高级次上。第二个问题用其它光学元件解决:在阶梯光栅后放置光栅、分光棱镜或其它色散元件,将不同波长/级次的光分开。

-
少年闪耀·初夏号(第4辑)
2025-09-28 14:41:07 查看详情


 求购
求购






