单连通空间

单连通空间(simply connected space)一类重要的拓扑空间.基本群为平凡群的道路连通空间称为单连通空间.从而可推出可缩空间是单连通空间，但是其逆不一定成立.例如，欧氏空间中的凸集和n维球面S" (n,2)都是单连通空间，但n维球面S"(n,2)不是可缩空间.道路连通空间是单连通的充分必要条件是，此空间中任意两条起点和终点分别相同的道路是同伦的.

非正式地说，如果我们的空间中有一个厚实的物体是由一块构成的，并且没有任何“洞”贯穿它，那么它就是简单的连接。例如，既不是甜甜圈也不咖啡杯（带把手）被简单地连接，但中空的橡胶球被简单地连接。在二维中，一个圆不是简单的连接，而是一个圆盘和一条线。被空间连接，但不是简单的连接被称为非简单的连接，或者在一个有点老式的长期，多重连接。

图1 示意图

图1中，一个球体被简单地连接起来，因为每一个环都可以被收缩（在表面上）到一个点上。

为了说明简单连通的概念，假设我们正在考虑一个三维的对象;例如，盒子形状的物体，面包圈或开瓶器。把这个物体想象成一个形状奇特的水族箱，里面装满了水，两边都是刚性的。现在想想一个潜水员拿一根长绳子，以任何方式在水族箱里面的水里落下来，然后把绳子的两端连接起来，形成一个闭环。现在循环开始收缩，变得越来越小。（假设这个循环魔术般地知道最佳的收缩方式，如果它可能避开它们的话，不会在锯齿状的边缘上挂钩）。如果循环可以一直收缩到一个点，那么水族馆的内部是简单地连接。如果有时环路被卡住了，例如在甜甜圈的中心孔周围，那么物体就不是简单的连接。

注意这个定义只排除了“手柄形”的孔。一个球体（或者相当于一个中空的橡皮球）是简单的连接的，因为球体表面上的任何环都可以收缩到一个点上，尽管它在中空的中心有一个“孔”。更强的条件，物体没有任何尺寸的洞，被称为收缩性。

这一套不是简单的连接，因为它有洞。

甲拓扑空间X被称为简单地连接，如果它是路径连接，并且任何连续地图˚F：S→X（其中S表示单位圆中欧几里德2空间）可以收缩以在以下意义上的点：存在连续映射F：D→X（其中D表示欧几里德2-空间中的单位盘），使得限于SF为f。

一个等价的表达式是这样的：当且仅当它是路径连通的时候，X是简单连通的，并且每当p：[0,1]→X和q：[0,1]→X是两条路径（即：连续映射）（p（0）=q（0）和p（1）=q（1）），那么p和q是同位相对{0,1}。直观地说，这意味着p可以“连续变形”来获得q，同时保持终点固定。因此，这个词简单地连接在一起：对于任何两个给定的点X，有一个“本质上”只有一条路径连接它们。

表达相同的第三种方式：当且仅当X是路径连接的，并且每个点上的X的基本组是平凡的，即仅由标识元素组成时，X是简单连通的。类似地，当且仅当X是所有态射集合中的所有点x，y时，X才被连接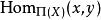在基本的广群的X只有一个元素。

在复杂分析中经常使用另一个公式：当且仅当黎曼球中的X和它的补数都连通时，C的开子集X是简单连通的。

虚数部分严格大于零且小于1的复数的集合提供了一个无限的，连通的，开放的补集未连接的平面子集的一个很好的例子。它是简单地连接。也许值得指出的是，放宽X连接的要求会导致对连接扩展补数的平面的开放子集进行有趣的探索。例如，一个（不一定是连接的）开放式集合在每个连接的组件都被简单地连接时就准确地连接了扩展式互补。

圆环不是简单的连接。没有任何一个彩色的圈可以收缩到一个点，不离开表面。

• 的欧几里得平面- [R被简单地连接，但ř减去原点（0,0）则不是。如果n> 2，则R和R两者都减去原点。
• 类似地：当且仅当n≥2时，n维球面S是简单地连通的。
• R每个凸子集都被简单地连接起来。
• 甲环面，所述（椭圆）气缸，所述莫比乌斯带，所述投影面与克莱因瓶不是简单地连接。
• 每个拓扑向量空间是简单连接的;这包括Banach空间和Hilbert空间。
• 对于Ñ≥2时，特殊正交群SO（Ñ，- [R）不是简单地连接和特殊酉群SU（Ñ）是简单连接。
• 的长行大号是简单连接，但它的紧凑化，延伸的长行大号*不是（因为它是不连通路连接）。
• 同样，R的单点紧化不是简单连接（即使R简单连接）。

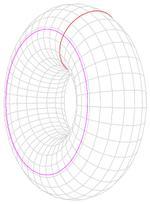图3 圆环连接

一个曲面（二维拓扑流形）是连通的，当且仅当它连通且它的属为0时。直观上，该属是曲面的“手柄”数。

如果一个空间X是不简单连接，经常可以通过使用其纠正这一缺陷普遍罩，映射到一个简单连接的空间X在一个特别好的方式。

如果X和Y是同伦等价的而X是简单的连接，那么Y也是。

请注意，连续函数下的简单连接集的图像不需要简单连接。以指数映射下的复平面为例：图像是C- {0}，显然不是简单的连接。

简单连通性的概念在复杂的分析中很重要，因为以下事实：

• 如果ü是的简单连接的开子集复平面Ç，和˚F：ü→Ç是一个全纯函数，然后˚F具有原函数˚F上ü，和每一个的值线积分在ü与积˚F仅取决于路径的终点u和v，并且可以被计算为F（v）-F（u）。积分因此不依赖于连接u和v的特定路径。
• 的黎曼映射定理指出的任何非空开单纯连接子集Ç（除了Ç本身）是共形等效到单元盘。

简单连通性的概念也是庞加莱猜想中的一个关键条件。