- 单连通区域

单连通区域
基础定义
先介绍平面曲线的有关概念。
定义1设平面曲线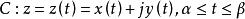 ,其中
,其中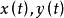 是实的连续函数,那么曲线C就称为连续曲线,
是实的连续函数,那么曲线C就称为连续曲线,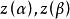 分别称为C的起点与终点,若在
分别称为C的起点与终点,若在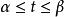 上,
上,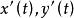 都连续且对每一个t,有
都连续且对每一个t,有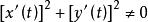 ,那么曲线C称为光滑曲线。由几段依次相接的光滑曲线所组成的曲线称为逐段光滑曲线。对于满足
,那么曲线C称为光滑曲线。由几段依次相接的光滑曲线所组成的曲线称为逐段光滑曲线。对于满足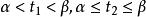 的
的![]() 与
与![]() ,当
,当![]() 且
且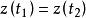 成立时,点
成立时,点![]() 称为曲线C的重点。没有重点的连续曲线C称为简单曲线或若尔当(Jardan)曲线。若简单曲线C的起点与终点重合,即
称为曲线C的重点。没有重点的连续曲线C称为简单曲线或若尔当(Jardan)曲线。若简单曲线C的起点与终点重合,即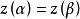 ,那么曲线C称为简单闭曲线。如图1所示。
,那么曲线C称为简单闭曲线。如图1所示。
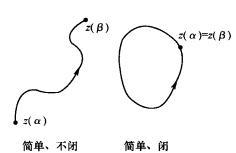 图1(a)
图1(a)
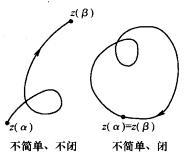 图1(b)
图1(b)
任意一条简单闭曲线C把整个复平面唯一地分成三个互不相交的点集,其中除去C以外,一个是有界区域,称为C的内部,另一个是无界区域,称为C的外部,C为它们的公共边界,简单闭曲线的这一性质,其几何直观意义是很清楚的。
定义2复平面上的一个区域D,如果在其中任作一条简单闭曲线,而曲线的内部总属于D,就称D为单连通区域(图2(a));一个区域如果不是单连通区域,就称为多连通区域(图2(b))。
一条简单闭曲线的内部是单连通区域(图2(a)),单连通区域D具有这样的特征:属于D的任何一条简单闭曲线,在D内可以经过连续的变形而缩成一点,而多连通区域就不具备这个特征。[2]
 图2(a)
图2(a)
 图2(b)
图2(b)
应用举例
单连通区域的一些性质
我们现在将概述单连通区域的一些性质,这些性质阐明它在全纯函数理论中起着重要作用。在这些性质中,(a)和(b)称为![]() 的内拓扑性质;(c)和(d)涉及
的内拓扑性质;(c)和(d)涉及![]() 嵌入s2内的方式;性质(e)到(h)按特征来说是分析性的;(i)是关于环
嵌入s2内的方式;性质(e)到(h)按特征来说是分析性的;(i)是关于环![]() 的代数陈述。[3]
的代数陈述。[3]
定理1对于一个平面区域![]() ,下面九个条件中的每一个蕴涵着其余的各个条件:
,下面九个条件中的每一个蕴涵着其余的各个条件:
(a)![]() 同胚于开单位圆盘U;
同胚于开单位圆盘U;
(b)![]() 是单连通的;
是单连通的;
(c)对![]() 内每一条闭路径
内每一条闭路径![]() 和对每一个
和对每一个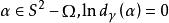 ;
;
(d)![]() 是连通的;
是连通的;
(e)每一个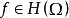 能用多项式在
能用多项式在![]() 的紧子集上一致逼近;
的紧子集上一致逼近;
(f)对每一个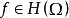 和在
和在![]() 内每一条闭路径
内每一条闭路径![]() ,
,
![]()
(g)每一个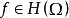 对应一个
对应一个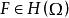 ,使得
,使得![]() ;
;
(h)如果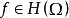 且
且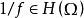 ,则存在一个
,则存在一个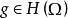 ,使得
,使得
![]()
(i)如果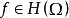 且
且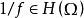 ,则存在一个
,则存在一个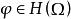 ,使得
,使得![]() 。
。
定理2如果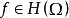 ,此处
,此处![]() 为平面内任意开集,且
为平面内任意开集,且![]() 在
在![]() 内没有零点,则
内没有零点,则![]() 在
在![]() 内调和。[3]
内调和。[3]
单连通区域内的柯西积分定理
定理3设![]() 在z平面上的单连通区域D内解析,C为D内任意一条围线,则[4]
在z平面上的单连通区域D内解析,C为D内任意一条围线,则[4]
![]()
推论1设![]() 在单连通区域D内解析,C为D内任意一条闭曲线(C不必为简单闭曲线),则
在单连通区域D内解析,C为D内任意一条闭曲线(C不必为简单闭曲线),则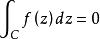 。
。
证明:由于闭曲线C总可以看成区域D内有限条周线衔接而成。因此,由复积分的曲线可加性及定理2即可得结论。
推论2设函数![]() 在单连通区域D内解析,则
在单连通区域D内解析,则![]() 在D内的积分与路径无关,即对D内任意两点
在D内的积分与路径无关,即对D内任意两点![]() 以及D内任意两条以
以及D内任意两条以![]() 为起点,
为起点,![]() 为终点的路径
为终点的路径![]() 和
和![]() ,总有
,总有
![]()

-
一汽丰田bZ4X正式上市 成都车展:奇瑞瑞虎5x西南区域上市
2025-11-02 01:35:23 查看详情 -
长安UNI 长安欧尚X5成都区域上市
2025-11-02 01:35:23 查看详情 -
长安欧尚X5成都区域上市 PLUS七座版内饰官图
2025-11-02 01:35:23 查看详情 -
长安要造最聪明的汽车 长安欧尚X5成都区域上市
2025-11-02 01:35:23 查看详情 -
长安欧尚X5成都区域上市 长安深蓝SL03正式亮相
2025-11-02 01:35:23 查看详情 -
长安欧尚X5成都区域上市 提供多种动力可选
2025-11-02 01:35:23 查看详情 -
长安欧尚X7 长安欧尚X5成都区域上市
2025-11-02 01:35:23 查看详情 -
长安欧尚X5成都区域上市 金额30亿元
2025-11-02 01:35:23 查看详情 -
长安欧尚X5成都区域上市 长安欧尚Z6预告图发布
2025-11-02 01:35:23 查看详情


 求购
求购

