- 仿射微分几何学

仿射微分几何学
基本内容
仿射微分几何学是微分几何学的一个分支,从属于仿射变换群。内容包括曲线和曲面在仿射变换群下的不变量、协变图形及其性质。兴起于20世纪20年代初,由德国数学家布拉施克等人创建。布拉施克的《微分几何讲义》(1921-1945) 第2卷专论仿射微分几何,得到仿射长度、仿射曲率、仿射挠率、仿射主法线、仿射副法线等与欧几里得几何同样的结果,还论述了仿射极小曲面,曲线、曲面的大范围性质等问题,其方法同射影微分几何学的富比尼方法相类似,分别使用了自然方程和基本微分形式,从而导出空间曲线和曲面论的基本定理。其基本思想源于C.F.克莱因的“埃朗根纲领”(1872年),即将几何学归结为可逆变换群的几何不变量理论加以分类,而讨论方法则依赖于高斯对曲面论所采取的基本形式[1]。
发展历程
20世纪20年代末期,仿射微分几何学的研究主要集中在仿射曲面论的几何结构、仿射铸曲面与仿射旋转曲面论的引进、仿射曲面论和射影曲面论间的若干关系等方面,使这门学科趋于完善。较早的专著有萨尔科夫斯基(E.Salkowski) 的《仿射微分几何》(1934)。到20世纪60 年代原苏联数学家希罗科夫出版专著《仿射微分几何学》(1962),汇总了这几十年的研究成果,并附有详细的文献表。中国数学家苏步青从20世纪20年代后期从事仿射微分几何学研究,发现了仿射铸面、仿射旋转面和某些特殊族的曲面,并发展了仿射曲面论,20世纪70年代又在计算几何中创造了仿射不变量理论,并应用于造船工业中的船体数学放样,收到显著效果。1982年他出版专著《仿射微分几何》,较完整地论述了这一学科的全貌,其中包括关于仿射曲面论的几何结构、仿射旋转面论及其在高维仿射空间的拓广和规范直线成为仿射法线的曲面族等方面的研究[1]。
仿射变换群
仿射变换群(affine transformation group)简称仿射群,是一类基本的变换群,即由仿射空间中全体仿射变换所构成的变换群。例如,平面上的全体仿射变换构成平面上的仿射变换群,它是平面射影变换中以无穷远直线为绝对形的自同构群。空间中全体仿射变换构成空间的仿射变换群,它是空间射影变换中以无穷远平面为绝对形的自同构群。研究在仿射群下不变性质与不变量的几何称为仿射几何。
微分几何学
微分几何学(differential geometry)简称微分几何,是数学的一个重要分支,主要研究可微分的形体(曲线、曲面、微分流形等)的几何性质。微分几何几乎与微积分同时产生和发展.当初,牛顿(I.Newton)和莱布尼茨(G.W.Leibniz)创立微积分的动机之一,就是为了解决计算一般曲线的切线和长度、曲线所围区域的面积等几何问题.微分几何的第一本著作当推蒙日(G.Monge)的《分析对几何的应用》,他和欧拉(L.Euler)及他们的学生们对微分几何的早期发展做出了重要贡献.曲面论的真正基础是由高斯(C.F.Gauss)奠定的,他于1827年出版了专著《关于弯曲曲面的一般研究》,书中证明:曲面的总曲率由它的第一基本形式完全确定。这就是曲面论的高斯方程,被称为极妙定理.从此以后,微分几何不再仅仅是微积分的一种应用,而成为数学的一个独立分支。
高斯建立的仅与曲面第一基本形式有关的内蕴几何是微分几何发展史上的一次关键性的突破,这一思想后来被黎曼((G.F.)B.Riemann)发扬光大.黎曼于1854年在格丁根大学发表了题为“关于作为几何学基础的假设”的就职演说,奠定了黎曼几何的基础.他发展了空间的概念,把后来称之为黎曼度量的对称正定二次微分形式赋予n维流形,并以此作为几何学的出发点.这就包括了一大类非欧几何(如椭圆几何、双曲几何(又称罗巴切夫斯基几何))。正是黎曼几何被爱因斯坦(A.Einstein)用来建立广义相对论,并且相对论反过来促进了黎曼几何学的发展。
克莱因(Klein,(C.)F.)于1870年在他的《埃尔朗根纲领》(Erlanger program)中提出,几何学应是研究空间在变换群作用下不变的性质.根据不同的变换群,就有欧氏几何、射影几何、仿射几何、共形几何等。这种用群论观点统一几何学的思想,在《埃尔朗根纲领》发表后的半个世纪内,成了几何学的指导思想.20世纪初期,射影微分几何的研究相当活跃,产生了以威尔辛斯基(E.J.Wilczynski)为代表的美国学派,以富比尼(G.Fubini)为代表的意大利学派和以苏步青教授为代表的中国学派。仿射微分几何和共形微分几何的决定性工作是由布拉施克(W.J.E.Blaschke)所做的.融黎曼和克莱因之思想于一体的是嘉当(E.Cartan),他把李群和微分几何结合起来,视联络为广义空间(纤维丛的前身)的主要几何对象,成功地发展了外微分理论和活动标架法.尤其是李群在流形上的作用,导致了齐性空间和对称空间的深入研究.这些都为现代微分几何奠定了基础。黎曼几何还有另外的推广,即把作为空间度量的正定二次型用更一般的正二次齐次函数来代替,其实这也是黎曼的本意。这种度量空间被芬斯勒(P.Finsler)、楞特(H.Rund)等发展成芬斯勒几何。
20世纪40年代以后,微分几何的一个发展趋势是研究空间或流形的整体性质,尤其是局部性质与整体性质的联系.著名的高斯-博内公式即是一例,陈省身在高维黎曼流形上的推广方面做出了重要贡献.霍奇(W.V.D.Hodge)的调和积分理论和德·拉姆(G.-W. de Rham)的上同调理论揭示了微分流形上微分结构、拓扑结构和黎曼结构之间的深刻联系,具有十分重要的意义.在一定几何条件下,根据调和理论,可用博赫纳(S.Bochner)方法得出各种消没定理.这就是所谓博赫纳技巧.黎曼流形上的测地线理论是整体黎曼几何学的核心之一。从测地线的无限延伸要求引出黎曼流形的完备性概念,霍普夫(H.Hopf)和里诺(W.Rinow)对此作出了贡献.完备性是整体微分几何研究中对流形所加的最起码和最自然的假设,它比紧致性更弱.测地线的变分理论导致了黎曼流形上各种曲率与拓扑的深刻结果.进一步的发展包括著名的球面定理,非负曲率的完备流形和非正曲率的紧致流形的结构等。测地线理论也促进了流形上分析的发展。
微分几何的另一重要研究方向是等距浸入和子流形几何。1926年,雅内特(N.Janet)和嘉当分别独立证明了任何n维解析黎曼流形均可局部等距嵌入到n(n+1)/2维欧氏空间中,但是,若去掉流形的解析性要求,问题至今尚未完满解决.尤其是高斯曲率变号的二维黎曼流形是否总可以局部等距嵌入三维欧氏空间中,仍是一个令人感兴趣的问题。关于整体等距嵌入问题,纳什(J.F.Nash)于1954-1956年给出了一般性结果:任何完备(紧致)黎曼流形均可整体等距嵌入到充分高维数的欧氏空间中作为子流形.纳什的方法后来对非线性分析产生重要影响.虽然有纳什的结果,但对于一个具体的黎曼流形,要确定它能等距嵌入进去的欧氏空间的最低维数,仍是一个相当困难的问题。黎曼流形的子流形几何是古典曲面论的直接推广,子流形的第二基本形式起着十分重要的作用.第二基本形式的迹称为子流形的平均曲率(向量).如同曲面论一样,平均曲率为零的子流形称为极小子流形.极小子流形具有明显的几何变分特征,它是体积泛函的临界点.极小子流形,特别是极小曲面,它们的整体存在性、惟一性和分类问题是子流形研究中最重要和最有吸引力的一个课题。
几何变分问题在现代微分几何中越来越占有重要的地位,这不仅在于它具有深刻的几何背景,而且还在于它和众多的其他数学分支相关联,如变分学、偏微分方程、近世代数、非线性分析、多复变函数论等。此外它还和理论物理、生物工程等相沟通。调和映射便是近年来发展十分迅速的一类几何变分问题.黎曼流形间的调和映射是其能量泛函的临界点.当起始流形为1维时便化为测地线.调和的等距浸入便是极小子流形.调和映射的第一个整体存在性定理是由伊尔斯(J.Eells)和桑普森(J.H.Sampson)于1964年共同给出的。从调和理论观点来看,调和映射是调和的1形式.其他重要的几何变分问题还有杨-米尔斯场、爱因斯坦度量、克勒-爱因斯坦度量等.它们不仅对现代微分几何学,而且对现代数学的发展都起了很大的促进作用。
微分几何是一门既古老又年轻的学科,它的新概念和新方法层出不穷.今天,无论在基础理论上还是在实际应用上,都日益显示出它的强大生命力.著名几何学大师陈省身教授说:“我希望它不要像其他一些数学分支那样被公理化.保持它跟数学中别的分支以及其他学科的许多领域的联系,保持着它把局部和整体相结合的精神。它在今后长时期中仍将是一片肥沃的疆域。”
仿射几何学
仿射几何学(affine geometry)是研究图形在仿射变换下不变性质的几何学。所谓仿射变换是仿射平面(或空间)到自身的一类变换,它最重要的特性是保持点的共线性(或共面性)以及保持直线的平行性。其中仿射空间是这样定义的:设V是一个n维向量空间,A是一个集合,其中的元素被称为点,如果对A中每两个点P、Q都唯一对应着V中的一个向量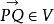 ,并且这种对应规则还满足:①
,并且这种对应规则还满足:①![]() (V中零向量);②任给P点和V中向量a,总唯一存在点Q使
(V中零向量);②任给P点和V中向量a,总唯一存在点Q使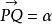 ;③对A中任意三点
;③对A中任意三点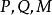 ,成立
,成立 ,则称A为一个n维仿射空间。
,则称A为一个n维仿射空间。![]() 时,称之为仿射平面。由此可见,仿射几何是一般欧氏几何的一种扩展。在仿射变换下,直线变为直线,平行直线变为平行直线,但长度与角的大小要改变。这种变换最先由18世纪瑞士数学家欧拉注意到,他在论述解析几何与微分几何的坐标变换时涉及到仿射坐标变换问题。19世纪初,德国数学家麦比乌斯在《重心的计算》(1827)一书中引入仿射几何的若干基本概念,并以浅显易懂和清晰严格的论述表达了这一新理论。他同时论述了射影几何理论,在仿射空间中引入无穷远点,并且将它们与原有点不加区别,就成为射影空间。由此可见,仿射空间是作为射影空间的一个特例进行讨论的。麦比乌斯用它来计算物体的重心,后人将它用于形变力学的研究。麦比乌斯引入的直射变换就是将直线变为直线的仿射变换,他证明了每一个直射变换都是一个射影变换。1872年德国数学家C. F.克莱因用变换群的观点研究几何学,将几何学看作是某种元素对于变换群的不变量理论。据此,射影几何学就是图形元素关于射影群不变量的理论,而仿射变换构成的群就成为射影变换群的一个子群。20世纪20年代仿射几何学再发新支,由研究曲线和曲面在仿射变换群下不变的性质而建立起仿射微分几何学,丰富了仿射几何学的内容[1]。
时,称之为仿射平面。由此可见,仿射几何是一般欧氏几何的一种扩展。在仿射变换下,直线变为直线,平行直线变为平行直线,但长度与角的大小要改变。这种变换最先由18世纪瑞士数学家欧拉注意到,他在论述解析几何与微分几何的坐标变换时涉及到仿射坐标变换问题。19世纪初,德国数学家麦比乌斯在《重心的计算》(1827)一书中引入仿射几何的若干基本概念,并以浅显易懂和清晰严格的论述表达了这一新理论。他同时论述了射影几何理论,在仿射空间中引入无穷远点,并且将它们与原有点不加区别,就成为射影空间。由此可见,仿射空间是作为射影空间的一个特例进行讨论的。麦比乌斯用它来计算物体的重心,后人将它用于形变力学的研究。麦比乌斯引入的直射变换就是将直线变为直线的仿射变换,他证明了每一个直射变换都是一个射影变换。1872年德国数学家C. F.克莱因用变换群的观点研究几何学,将几何学看作是某种元素对于变换群的不变量理论。据此,射影几何学就是图形元素关于射影群不变量的理论,而仿射变换构成的群就成为射影变换群的一个子群。20世纪20年代仿射几何学再发新支,由研究曲线和曲面在仿射变换群下不变的性质而建立起仿射微分几何学,丰富了仿射几何学的内容[1]。



 求购
求购









