双向方差分析

1925年，Ronald Fisher在他1925年的着名书籍“研究工作者统计方法”（第7章和第8章）中提到了双向方差分析。1934年，弗兰克耶茨发布了不平衡案件的程序。从那时起，已经产生了大量的文献。这个话题在1993年由Yasunori Fujikoshi审查。2005年，安德鲁Gelman提出了一种不同的ANOVA方法，被视为一种多级模型。

想象一个数据集，其中一个因变量可能受到两个潜在变异因素的影响。第一个因素有水平(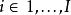)和第二个\水平(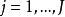)。每个组合定义一种治疗方法，总共为治疗。我们代表治疗的重复次数通过， 然后让作为该处理中重复的指标（）。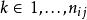

从这些数据中，可以建立一个应急表，其中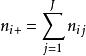，和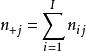，并且重复的总数等于 。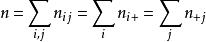

该实验设计是平衡的，如果每次治疗具有相同数量的重复的，。在这种情况下，设计也被认为是正交的，从而可以完全区分这两种因素的影响。因此我们可以写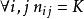和。

一旦观察到变异数据点，例如通过直方图，“概率可能被用来描述这种变化”。因此让我们表示观察值的随机变量是第个治疗措施。该双向方差分析模型中的所有这些变量变化的独立和通常围绕一个平均值，具有不变的方差：

具体而言，响应变量的均值被建模为解释变量的线性组合：

这里表示总平均，是等级的附加主效应从第一个因素（第一个在contigency表中的行），是等级的附加主效应从第二个因素（第j个列在contigency表）和是治疗的非加性相互作用效应来自这两个因素（第行第列和第列在contigency表中）。

描述双因素方差分析的另一种等效方法是提及除了因素解释的变化之外，还存在一些统计噪音。通过在每个数据点引入一个随机变量来处理这种未解释的变化量，，称为错误。这些随机变量被视为与平均数的偏差，并被假定为独立正态分布：

在Gelman和Hill之后，ANOVA的假设以及更一般的一般线性模型按重要性递减顺序：

1）数据点与调查中的科学问题有关；

2）响应变量的平均值受累加性影响（如果不是相互作用项），并且受到因素的线性影响；

3）错误是独立的；

4）错误具有相同的方差；

5）错误是正态分布的。

为了确保参数的可识别性，我们可以添加下面的“总和到零”约束：