- 引力量子场论

引力量子场论
基本概述
引力量子场论的建立基于自然界基本规律与时空坐标和标度选取无关且遵循局域规范不变原理。自然地引入双标架四维时空概念,即具有整体庞加莱和标度对称性的四维坐标时空以及具有局域自旋和标度规范对称性的四维引力场时空,前者描述量子场的运动和度量,后者决定量子场的内禀自由度和相互作用。在引力量子场论中,引力相互作用由自旋规范对称性SP(1,3)支配,基本引力场不再是弯曲坐标时空的几何度规,而是双标架四维时空中的双协变规范矢量场,它耦合到所有量子场,形成的局域平坦四维引力场时空由非对易几何来刻画。
引力量子场论给出了统一描述引力、电磁力、弱力、强力、自旋力和标度力的一个基本理论框架,可导出含有引力场效应的所有量子场运动方程和所有基本对称性对应的守恒定律。爱因斯坦广义相对论作为引力量子场论中引力场方程的对称部分而呈现。此外,引力量子场论中的量子效应使得引力标度子引发整体标度对称性破缺从而导致早期宇宙暴胀,给出以量子暴胀宇宙为起源的量子引力场时空动力学。引力量子场论的建立不仅对理解宇宙的起源和演化至关重要,而且对量子理论本身的普适性和自洽性起着根本性作用。
提出动机
目前,已知自然界存在四种基本相互作用:电磁、弱、强和引力相互作用。前三种相互作用由平直闵氏时空中的相对论量子场论描述,由规范对称性刻画,称为粒子物理标准模型。引力在宏观世界由爱因斯坦提出的广义相对论描述。广义相对论是构建在黎曼度规下的弯曲时空动力学。显然,这种构建在弯曲时空中的度规动力学不同于其它三种基本相互作用力的处理方式。从而很难构建一种统一描述引力及其它三种基本相互作用的理论,以至于引力量子化变得异常困难。
在过去半个世纪里,众多理论物理学家尝试构建引力规范理论,但几乎所有尝试都基于弯曲时空的黎曼或非黎曼几何。另一方面,研究表明,在基于整体平坦时空的量子场论框架下统一描述引力对理解和探索宇宙起源起到越来越重要的作用,如奇点问题、早期宇宙暴涨等。如何基于整体平坦闵氏时空中的量子场论框架建立一种新的引力规范理论,使之从根本上与电磁作用、弱作用和强作用进行平等和统一地描述。即所有基本粒子的相互作用均由规范对称性支配且由定义在整体平坦的闵氏坐标时空中的量子场来刻画。
建立基础
狭义相对论和量子力学的成功统一建立了相对论量子场论,成为描述微观世界的基本理论框架。结合对称原理,即对称性和对称破缺,建立起描述基本粒子的相对论量子场论。研究表明,规范对称性决定相互作用,规范对称破缺导致物质质量的产生。由此,在整体平坦时空的量子场论框架下,建立起描述电磁、弱和强相互作用的粒子物理标准模型,对应的对称性分别为:U(1)Yx SU(2)Lx SU(3)c。这些对称群在数学上称为幺正李群。
爱因斯坦广义相对论的建立基于广义协变原理:即自然界的物理定律由一组方程来描述,它们在所有坐标系下都是很好定义的,具有广义坐标不变性。数学上由广义线性群GL(4,R)所对应的对称性来描述。在爱因斯坦广义相对论中,引力场由弯曲时空的度规场来描述。如果时空度规作为引力场是有限且正定的,爱因斯坦表明,人们总能选择一个特殊的坐标系使得度规矩阵的行列式数值为1,由此可大大简化引力场运动方程。但问题在于,如果选择了这一特殊的坐标系,就没有广义坐标不变性,似乎意味着要放弃广义协变原理。但爱因斯坦在《广义相对论基础》这篇论文中是这样考虑的:认为这样做就意味着部分地放弃广义相对论假设是不对的。因为我们并不会问“对所有行列式为1的变换都协变的自然规律是什么?” 我们的问题是 “什么是广义协变的自然规律?”。只是当我们公式化后,才选取特殊的坐标系简化我们的表达式。
1915年建立广义相对论必然受到当时对自然规律认识的局限性。那时,量子力学还没有建立,更不用说量子场论。对于物质的基本组成,除电子外,其它的基本组元,即6种夸克和6种轻子都一概不知。同样,除电磁力和引力外,并不知道弱和强相互作用力的存在。爱因斯坦通过推广狭义相对论成功地建立广义相对论来描述引力,既是一个自然的推广,也是科学上的一个创举。爱因斯坦引力场方程首次建立起了时空几何与物质间的相互关联。
1928年,狄拉克把狭义相对论与非相对论性量子力学结合建立了相对论性量子力学。相对论性量子力学的狄拉克方程给了人们更多的启示:当把时间与空间联系在一起作为四维时空进行平权处理时,描述基本粒子的波函数不再是标量场而是4-分量的狄拉克旋量场。这意味着时空的4个维度对应于物质场的4个分量,进一步阐明了时空的基本性质与物质的内禀自由度之间的几何联系。这之后,发展了相对论性量子场论和粒子物理标准模型。粒子物理取得了许多突破性进展,例如:建立量子电动力学(QED)、提出Yang-Mills规范理论、发现宇称不守恒、建立电弱统一模型、发现夸克和轻子、建立量子色动力学(QCD)。
当把以弯曲时空动力学为基础的广义相对论与建立在整体平坦时空中的相对论量子场论结合时,却遇到了难以逾越的一些理论障碍:弯曲时空不再具有四维时空的整体平移和转动不变性,不能很好地定义能量、动量和角动量等物理守恒量,也无法像狭义相对论那样很好地定义时间和空间间隔。基于时空坐标广义线性群GL(4,R)局域对称性所建立的广义相对论与基于基本粒子量子场幺正规范对称性U(1)Yx SU(2)Lx SU(3)c建立的粒子物理标准模型,显然无法在同一层次上进行统一描述。然而,建立在量子场论框架上的粒子物理标准模型和基于广义协变原理的广义相对论都得到了已有实验的验证。
这使得理论物理学家面临着一个长期未决的基本问题:能不能基于整体平坦时空的量子场论框架来描述引力相互作用?也就是说能否建立起不基于广义协变原理的引力理论?要解答这个问题,自然要求超越爱因斯坦广义相对论的基本假设。
对这个基本问题的探索导致吴岳良打破爱因斯坦广义相对论中关于广义坐标变换不变假设的局限,不再从推广狭义相对论和坐标时空几何的途径来构建量子引力理论,而是基于量子场论和规范对称原理,建立超越爱因斯坦广义相对论的引力量子场论。
基本假设和原理
依据规范对称原理,规范对称性决定相互作用。而对称性的引入与构成自然界的基本组元(如夸克和轻子)的内禀自由度紧密相关。引力量子场论的建立是在量子场论理论框架下基于以下的基本假设和原理:
(i)将费米子量子场的自旋对称群SP(1,3)作为一种内部对称性,区别于闵氏时空中坐标的洛伦兹对称群SO(1,3);
(ii)所有量子场的运动学需遵循狭义相对论和量子力学原理;
(iii)所有量子场的动力学由规范对称性支配的基本相互作用来刻画;
(iv)引入双标架时空(biframe)概念,其中一个时空标架是整体平坦的闵氏时空,它起着惯性参考系的作用,用以描述基本场的运动,并很好地定义守恒量;另一个标架是局域平坦的非坐标引力场时空,它用于表征相互作用,刻画场的动力学;
(v)在引力场时空中构建规范不变和时空坐标无关的量子引力作用量。
由此得到的引力量子场论不仅具有在局域平坦引力场时空中的自旋和标度规范变换不变性,并且具有在整体平坦闵氏坐标时空中的庞加莱(非齐次洛伦兹)和标度变换不变性。
基本性质和研究内容
引力量子场论的一些基本性质和研究内容:
(1)基本引力场是定义在局域平坦非坐标四维时空和整体平坦四维闵氏坐标时空的双协变矢量场![]() (X)。 这里的矢量场
(X)。 这里的矢量场![]() (X)是伴随基本粒子量子场具有局域自旋规范对称性SP(1,3) 和标度规范对称性时而引入的双协变矢量场,其对偶场 耦合到所有量子场的动力学项和规范相互作用项;
(X)是伴随基本粒子量子场具有局域自旋规范对称性SP(1,3) 和标度规范对称性时而引入的双协变矢量场,其对偶场 耦合到所有量子场的动力学项和规范相互作用项;
(2)由双协变矢量引力场形成的非坐标时空是一个局域平坦引力场时空,由对偶引力场基{
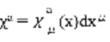 公式
公式
和
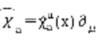 公式
公式
刻画。局域平坦引力场时空具有非对易几何特性,并由引力场强刻画。矢量场
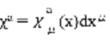 公式
公式
作为定义在整体平坦闵氏时空的规范势,其场强描述引力相互作用;
(3)量子场论中整体平坦闵氏时空提供一个惯性系以描述量子场运动;且能很好地给出动量和能量等守恒量的定义,可导出所有量子场的运动方程。通过与守恒的能动量张量相联系得到引力场的运动方程;
(4)当自旋和标度规范对称性破缺到具有整体洛伦兹和标度对称性的背景时空结构时,在固定标度规范条件定义的幺正基下,可求解得到背景场运动方程的严格解;
(5)引力场时空的几何特征通常由度规场和标度场刻画。得到的背景引力场时空具有洛伦兹不变性,是一类共形平坦的闵氏时空。背景引力场时空由具有非零宇宙质量标度的宇宙矢量来刻画。背景引力场时空对共形固有时而言不再是各向同性的,只有在共动坐标系框架下才显得各向同性。就共形固有时或共动坐标系而言,当光运动接近宇宙视界时,宇宙共形标度将变为无穷大,但以宇宙固有时作为时间度量,需要无穷长时间才能达到宇宙视界。只有以宇宙固有时作为时间度量时,早期宇宙呈现暴涨的性质。宇宙暴涨的发生可由引力量子场论的量子效应引起。
标度规范不变性允许在幺正基下(基本引力场的行列式为1)构建量子化的引力相互作用。规范固定对于引力规范理论量子化的贡献表现为利用路径积分方法下的Faddeev-Popov形式。类似于Yang-Mills规范理论量子化,引力量子场论在确认物理自由度以及量子引力理论定义时,不存在任何困难。基于背景引力场时空,通过给出领头项的有效作用量,可推导得到费曼规则并研究引力量子效应。因规范型引力场的对偶场耦合到所有量子场而产生非线性相互作用,甚至导致无穷大使得理论不可重整性。另一方面,具有标度规范不变的引力相互作用,且局域平坦引力场时空是非对易的,表明存在一个由理论的紫外行为所表现的基本能标,因此通过很好地定义和正规化发散积分,可使得理论变成有限且是有意义的,如:2003年由吴岳良发展的圈正规化方法。当自旋和标度规范对称性破缺到具有整体洛伦兹和标度对称性的背景时空结构时,会出现与背景场耦合而导致的极其丰富的引力相互作用。基于标度子有效背景标量势的单圈量子贡献可探讨宇宙暴涨的量子效应,其量子效应的二次型贡献可引发整体标度对称性破缺,引发早期宇宙暴涨。当背景场标量势真空期望值演化到稳定的极小值时,宇宙暴涨效应停止。
当把引力场作为类Goldstone场使得局域自旋规范对称性成为隐性对称性,理论呈现整体洛伦兹对称性,可由自旋规范场构建对应的时空规范场:
![]() 公式
公式
,这里自旋规范对称性变为一种隐性规范对称性。这里时空规范场可定义在平坦闵氏时空下的一种洛伦兹张量场,由此可给出另一种等效形式的量子引力作用量。理论表明,玻色子量子场的引力相互作用可由类Goldstone引力度规场以及时空规范场来描述,但引力场同费米子量子场的相互作用除外。只有当自旋规范固定到幺正规范条件时,即通过自旋规范变换使得双协变矢量引力规范场成为对称的张量,基本引力场与度规场具有相同的自由度,引力量子场论的两种形式才完全等价。由此,可将规范引力量子场论与爱因斯坦广义相对论进行比较,从而得到几何引力场方程:一组对应于爱因斯坦广义相对论的引力场方程,由对称的能动量张量支配;另一组引力场方程是超越爱因斯坦广义相对论的引力场方程,由反对称能动量张量支配。
引力量子场论给出了统一描述引力、弱力、电磁力和强力四种相互作用力的一个理论框架,如何把四种基本相互作用力统一成为一种基本相互作用成为理论物理学家追求的梦想。在引力量子场论框架下,2017年吴岳良基于时空维度与基本量子场自由度之间的相干关联,建立了高维超时空中的统一场论,表明了支配所有基本相互作用力的超自旋规范对称性具有其引力起源。

-
宇宙之海的涟漪:引力波探测
2025-09-22 04:41:17 查看详情 -
星力量(北京)国际文化传媒有限公司
2025-09-22 04:41:17 查看详情 -
长城炮带你清凉一夏 中国皮卡最强力量
2025-09-22 04:41:17 查看详情 -
长城风骏5助力开创美好生活 中国皮卡最强力量
2025-09-22 04:41:17 查看详情 -
皮卡顶流长城炮 中国皮卡最强力量
2025-09-22 04:41:17 查看详情 -
长城炮破圈拓界解锁新玩法 中国皮卡最强力量
2025-09-22 04:41:17 查看详情 -
长城炮带你开启浪漫之旅 中国皮卡最强力量
2025-09-22 04:41:17 查看详情


 求购
求购




