矩阵转置

设A为m×n阶矩阵（即m行n列），第i 行j 列的元素是a(i,j)，即：A=a(i,j)

定义A的转置为这样一个n×m阶矩阵B，满足B=b(j,i)，即 a(i,j)=b (j,i)（B的第i行第j列元素是A的第j行第i列元素），记A'=B。(有些书记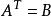为，这里T为A的上标）

直观来看，将A的所有元素绕着一条从第1行第1列元素出发的右下方45度的射线作镜面反转，即得到A的转置。

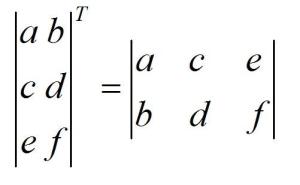矩阵转置例：

矩阵转置(3)(A±B)T=AT±BT

(A×B)T= BT×AT

(AT)T=A

(KA)T=KAT

设A为n阶矩阵，如果满足A^T=A

，即

那么A称为对称矩阵。