- 上确界

上确界
定义
序理论
上确界是序理论中最基础的概念之一。
给定偏序集(S, ≤),A是S的子集,则A的上确界(亦称最小上界)supA定义为满足以下条件的元素:
Ⅰ.supA∈S
Ⅱ.∀a∈A⇒a≤ supA
Ⅲ.∀a∈S,若a满足∀b∈A⇒b≤a,则supA≤a。
即:supA是A的所有上界组成的集合的最小元(若存在)。
A的上确界亦被记为sup(A),lubA,LubA或∨A。
上确界在序理论中的对偶概念是下确界。
并非所有的A都能找到上确界。
数学分析
具体到数学分析中。一个实数集合A,若有一个实数M,使得A中任何数都不超过M,那么就称M是A的一个上界。在所有那些上界中如果有一个最小的上界,就称为A的上确界。[1]即设有一实数集A⊂R,实数集A的上确界supA被定义为如下的数:
(1) (即supA是A的上界)
(即supA是A的上界)
(2) (即再小一点就不是上界)
(即再小一点就不是上界)
一个数集若有上界,则它有无数个上界;但是上确界却只有一个,这可以直观地从上确界(最小上界)的含义中看出来。并且如果一个数集若有上界,则它一定有上确界。[2]
常用结论
确界定理
在一般的数学分析学教材中,实数理论一章,为了说明实数的紧性,有一系列的定理,理论比较严密的前苏联教材一般是以戴德金分割定理为出发点证明其它的等价定理。而我国教材为了简化,很多都是从确界定理为出发点进行的证明,其他说明实数的连续性的定理还有区间套定理,有限覆盖定理等等。[3]
确界定理是实数理论中最基本的结论之一,是实数集紧性的体现。
定理:任何有上界(下界)的非空实数集必存在上确界(下确界)。
证明
用戴德金分割定理证明。
戴德金分割定理:对实数集R的任意一个满足不空、不漏、不乱的划分A和B,都存在唯一的一个分点![]() 满足
满足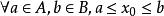 。
。
记给定非空集合为X。取定B为X的所有上界的集合,A=R\B。下证A、B为划分。
不空:由于X非空,可取![]() ,易知x-1不可能为X的上界,故A非空。B非空给定;
,易知x-1不可能为X的上界,故A非空。B非空给定;
不漏:由A=R\B知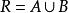 ;
;
不乱:设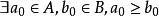 ,则由
,则由![]() 知
知![]() 不是X的上界,即
不是X的上界,即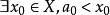 ,但又由
,但又由![]() 是X的上界知
是X的上界知 ,综上,
,综上,![]() 又
又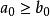 ,矛盾。不乱得证。
,矛盾。不乱得证。
故存在唯一的一个分点![]() 满足
满足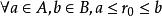 。下证分点为上确界,即
。下证分点为上确界,即![]() 。
。
若不然,![]() ,则
,则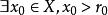 ,但此时就有
,但此时就有![]() ,由
,由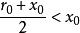 知
知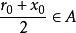 ,与
,与![]() 是划分A和B的分点相矛盾。故
是划分A和B的分点相矛盾。故![]() 。
。
下确界同理。证毕。



 求购
求购
