抛射体运动

抛射体的理想运动 指在下述四种假设下的运动：①抛射体在真空中运动；②抛射体的射程与地球的尺寸相比很小，故地球表面可视为平面，各处重力互相平行；③抛射的高度与地球半径相比很小，各处重力加速度g 可视为常数且等于在地面的值；④在地面上静止的物体具有与地球在该点的转动速度相同的速度，所以初速不太大时，抛射体的运动可不考虑地球的转动。在这些假设下，抛射体对静止于地面的直角坐标系的运动方程为：

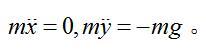
设初速与水平成角，而初始条件为：

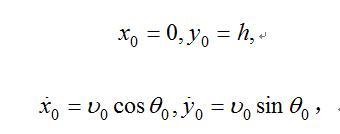
则积分后的运动方程为：

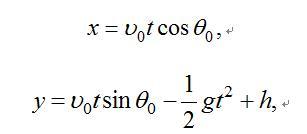
消去t后，得弹道方程：

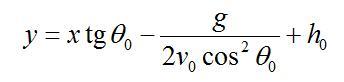
这是一个抛物线方程（图1）。当y=h时，可从上式求出抛射体的射程：

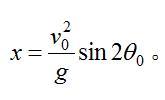
可见射程不仅与初速度v0有关，且与θ0有关。当θ0=45°时，射程最大。

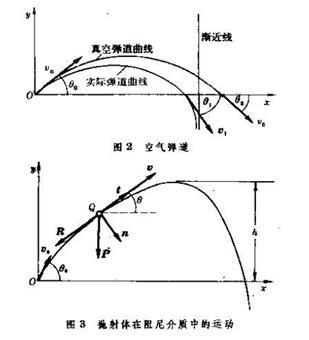
考虑空气阻力的抛射体运动，炮弹或导弹在空气中运动时，空气的阻力对弹道的影响 是缩短射程、减小落地速度和增大落地角，并使弹道具有竖直渐近线 （图2）。

在阻尼介质中运动的抛射体同时受到重力P和空气阻力R的作用（图3）。R与速度v反向，其大小则为0的 某一函数mf（v）,其中m为抛射体的质量,是为了算式简明而写上的。抛射体沿曲线的切向和法向的运动微分方程为：

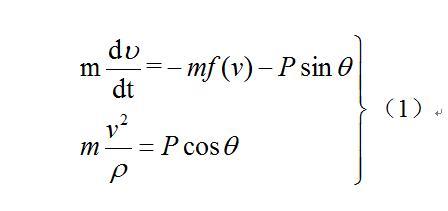
式中θ是速度矢量与水平轴x的夹角。

曲率半径ρ与弧长s和倾角θ有如下关系：

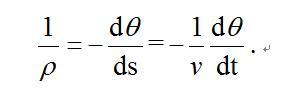
式中负号表明θ角随弧长s的增加而减小。于是式（1）可写作：

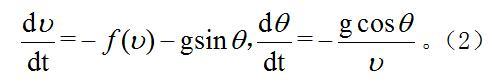
从以上两式消去dt，得到：

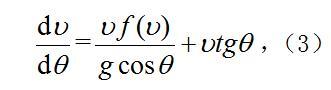
或改写为：

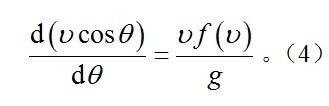
只有在函数f（v）取某些特殊形式时，式（3）才有一般的积分。

下面分述介质阻力对抛射体运动的影响。

将式（4）写为：

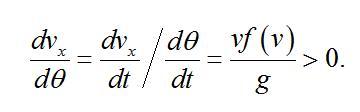
由于

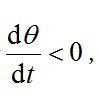
推出

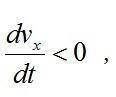
即速度的水平分量是减函数，故射程比理想运动时要短。

利用式（2）的第二式，

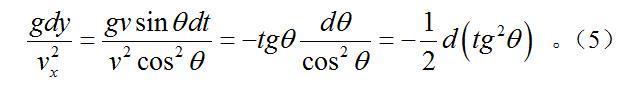
沿弹道的上升段积分，y由0到h，θ由θ0到0,得到：

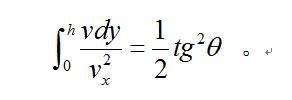
如以θ1代表落地角，将式（5）沿下降段积分，得到：

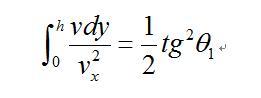
因为是减函数，上面第二个积分的值必定大于第一个，故

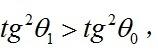
即抛射体的落地角θ1大于发射角θ0。

将式（2）的第一式乘以v并积分，得：

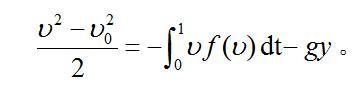
设落地时t=t1，落地速度为v1，此时y=0,上式变为：

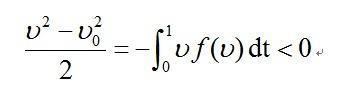
此式表明v1<v0,即落地速度v1小于发射速度v0。

θ角从初始值逐渐减小，在弹道顶点处变为零，此后即取负值。由式（2） 中的第二式得出：

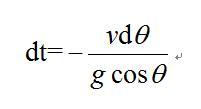
根据初始条件t=0时θ=，积分后可得：

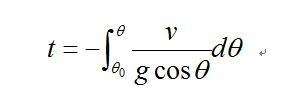
从上式可以看出，当

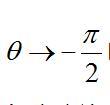
时

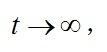
故在阻尼介质中弹道具有竖直渐近线。

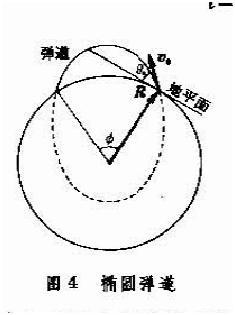
此外，当射程较大时,例如远程弹道导弹，由于地面是球形，球面曲率的影响是增大射程（图4）。图中椭圆是导弹在地球有心力场中的真空弹道。此时的射程等于，显然大于设地面为平面情况下的射程。

词条作者：黄克累．《中国大百科全书》74卷（第一版）力学 词条：抛射体运动：中国大百科全书出版社， 1987 ：377-378页．

相关连接