- 素数普遍公式

素数普遍公式
公式
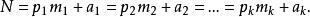 ...(1)
...(1)
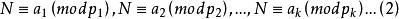
目录
- 1一、引言
- 2二、素数普遍公式
1、引言
2000多年前欧几里德在证明素数无穷多时就埋下了寻求素数普遍公式的伏笔,以布劳维尔为首的直觉主义学派认为:“你没有给出第n个素数是如何构造的,就不能算是好的证明”。2000多年来,数论学最重要的一个任务,就是寻找素数普遍公式,为此,一代又一代数学精英,耗费了巨大的心血,始终未获成功。黎曼曾想用他的ζ函数数的“零点”来逼近素数普遍公式,至今未获成功。也有人反向思考,用素数普遍公式逼近“零点”来解决黎曼猜想。希尔伯特在1900年的国际数学家大会上说:对黎曼公式进行了彻底讨论之后,或许就能够严格解决哥德巴赫问题和孪生素数问题。实际在哲学上,只要有一个明确的定义,就应该有一个公式[1]。
2、素数普遍公式
公元前250年同样是古希腊的数学家埃拉托塞尼提出一种筛法:
(一)“要得到不大于某个自然数N的所有素数,只要在2---N中将不大于![]() 的素数的倍数全部划去即可”。
的素数的倍数全部划去即可”。
(二)将上面的内容等价转换:“如果N是合数,则它有一个因子d满足1<d≤![]() ”。(《基础数论》13页,U杜德利著,上海科技出版社)。.
”。(《基础数论》13页,U杜德利著,上海科技出版社)。.
(三)再将(二)的内容等价转换:“若自然数N不能被不大于![]() 的任何素数整除,则N是一个素数”。见(代数学辞典[上海教育出版社]1985年。屉部贞世朗编。259页)。
的任何素数整除,则N是一个素数”。见(代数学辞典[上海教育出版社]1985年。屉部贞世朗编。259页)。
(四)这句话的汉字可以等价转换成为用英文字母表达的公式: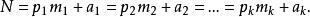 ...(1)
...(1)
其中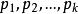 表示顺序素数2,3,5,,,,,。
表示顺序素数2,3,5,,,,,。![]() 。若N<
。若N<![]() ,则N是一个素数。
,则N是一个素数。
(五)可以把(1)等价转换成为用同余式组表示: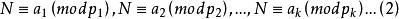
由于(2)的模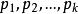 两两互素,根据孙子定理(中国剩余定理)知,(2)在
两两互素,根据孙子定理(中国剩余定理)知,(2)在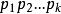 范围内有唯一解。
范围内有唯一解。
例如k=1时,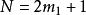 ,解得N=3,5,7。求得了(3,
,解得N=3,5,7。求得了(3,![]() )区间的全部素数。
)区间的全部素数。
k=2时,
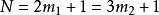 ,解得N=7,13,19;
,解得N=7,13,19;
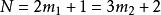 ,解得N=5,11,17,23。求得了(5,
,解得N=5,11,17,23。求得了(5,![]() )区间的全部素数。
)区间的全部素数。
| k=3时 | 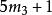 |
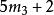 |
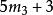 |
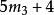 |
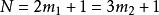 |
31 | 7; 37 | 13; 43 | 19 |
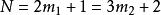 |
11; 41 | 17; 47 | 23 | 29 |
求得了(7,![]() )区间的全部素数。
)区间的全部素数。
由孙子定理知,(1)式和(2)式在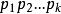 范围内有(2-1)(3-1)(5-1)....(
范围内有(2-1)(3-1)(5-1)....(![]() -1)个解。
-1)个解。
两式的本质是从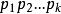 中除去pm(m〉1)的合数,这一点与埃拉托塞筛法不同,埃氏筛是用
中除去pm(m〉1)的合数,这一点与埃拉托塞筛法不同,埃氏筛是用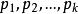 去筛
去筛![]() 以内的合数,剩下的就是
以内的合数,剩下的就是![]() 以内的素数了。
以内的素数了。
例如用2,3,5,去筛49以内的合数,剩下的就是(7,![]() )区间的素数了。但是,(1)(2)式是用
)区间的素数了。但是,(1)(2)式是用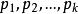 去筛
去筛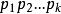 以内的pim(i≤k)形的数,连同模
以内的pim(i≤k)形的数,连同模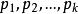 也筛掉了。
也筛掉了。
切比雪夫证明了“![]() <
<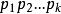 对于由4开始的所有的K 都是对的。例如,
对于由4开始的所有的K 都是对的。例如,![]() >2,
>2,![]() >2×3,
>2×3,![]() >2×3×5,
>2×3×5,![]() <2×3×5×7。从11开始都是这样了。(参见[数学欣赏]汉斯拉德海著220页“数30的一个性质”北京出版社1981.6)所以,若K≥4时,(1)(2)式的计算结果只能取
<2×3×5×7。从11开始都是这样了。(参见[数学欣赏]汉斯拉德海著220页“数30的一个性质”北京出版社1981.6)所以,若K≥4时,(1)(2)式的计算结果只能取![]() 以内的值才是素数。
以内的值才是素数。
仿此下去可以一个不漏地求得任意给定数以内的全部素数。求得了(11,![]() )区间的全部素数。 共有(2-1)×(3-1)×(5-1)×(7-1)=48个解。 小于11平方的解。
)区间的全部素数。 共有(2-1)×(3-1)×(5-1)×(7-1)=48个解。 小于11平方的解。
3,孪生素数问题
公式[2]孪生素数有一个十分精确的普遍公式,利用素数判定法则:“若自然数![]() 与
与![]() 都不能被不大于
都不能被不大于![]() 的任何素数整除,则
的任何素数整除,则![]() 与
与![]() 是一对素数,称为孪生素数。这一句话用数学语言表达就是:
是一对素数,称为孪生素数。这一句话用数学语言表达就是:
存在一组自然数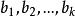 使得:
使得:
 ......(4)
......(4)
其中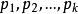 表示顺序素数2,3,5,....。
表示顺序素数2,3,5,....。
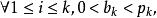
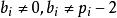 。
。
若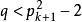 ,,则
,,则![]() 与
与![]() 是一对孪生素数。
是一对孪生素数。
上式可以用同余式组表示:
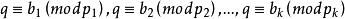 ......(5)。
......(5)。
由于(2)式的模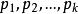 两两互素,根据孙子(中国剩余)定理,对于给定的b值,(2)式在
两两互素,根据孙子(中国剩余)定理,对于给定的b值,(2)式在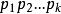 范围内有唯一的解。
范围内有唯一的解。
范例
例如,k=1时,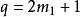 ,解得
,解得![]() =3和5,5<
=3和5,5<![]() ,得知3与3+2,5与5+2是两对孪生素数。从而得到了
,得知3与3+2,5与5+2是两对孪生素数。从而得到了![]() 区间的全部孪生素数。
区间的全部孪生素数。
k=2时,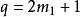 =
=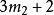 。解得
。解得![]() =5,11,17。17<
=5,11,17。17<![]() ,得知11与11+2,17与17+2是孪生素数对,从而得到
,得知11与11+2,17与17+2是孪生素数对,从而得到![]() 区间的全部孪生素数。
区间的全部孪生素数。
推论孪生素数猜想就是要证明(4)式或者(5)式在k值任意大时都有小于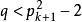 的解[3]。
的解[3]。

-
油耗怎么计算(油耗怎么计算公式多少钱一公里)
2025-09-22 06:15:33 查看详情 -
百公里油耗多少钱(百公里油耗多少钱怎么算公式)
2025-09-22 06:15:33 查看详情 -
怎么算油费(怎么算油费公式)
2025-09-22 06:15:33 查看详情 -
汽车油耗怎样计算(汽车油耗怎样计算公式)
2025-09-22 06:15:33 查看详情 -
发动机功率计算公式 发动机功率的计算公式及单位换算
2025-09-22 06:15:33 查看详情 -
百公里油耗计算器公式
2025-09-22 06:15:33 查看详情


 求购
求购





